Inicio / Archivo / Año 5, No 5, septiembre 2022 - agosto 2023 / Paper 04

---

UNA PROPUESTA DE LAS MATRICES DE ROTACIÓN PARA EL
MANEJO DEL DRIFT

Gabino Estevez-Delgado^*, Joaquín Estevez-Delgado, Victoria Belen Palomares-Rizo
¹Universidad Michoacana de San Nicolás de Hidalgo
^*gabino.estevez@umich.mx

Resumen

Cuando se trata de servicios de calidad acreditados bajo la referencia internacional ISO 17025, cuya área de aplicación es dada para los laboratorios de ensayos y calibración, existen dos parámetros, la incertidumbre y error de medición. Caso de atención particular es la incertidumbre la cual deben de identificar las variables de influencia que intervienen en la medición y que generan la variabilidad más importante. Es esta variable la que motiva la presente investigación en la que una de las variaciones que se identifican el DRIFT, que a diferencia de otras variables que influyen en las mediciones, tienen un comportamiento en el que el valor esperado equivalente al valor promedio crece con una pendiente que se incrementa en el tiempo. El análisis de esta variabilidad es motivado no solo por la propia referencia ISO 17025, y la guía internacional para evaluar la incertidumbre, sino que existen otras exigencias de valoración como lo es la calificación metrológica que ha ido en aumento como una necesidad por parte de las organizaciones, tantos laboratorios y la industria o aquellos que utilizan el método CEIMA (Calificación de Equipos de Instrumentos de Medición Analítica). La investigación realizada consiste atender la variabilidad de los cromatógrafos llamada DRIF a través de la generación de las curvas trasladadas rotacionalmente a un eje paralelo al eje de las x, para posteriormente poder atender las coordenadas a valores usados mediante el método de mínimos cuadrados para el caso de la regresión lineal. Esta metodología nos lleva al tratamiento de los datos no solo para el análisis de la variabilidad, sino el tratamiento de posibles valores que pueden generar riesgos en los procesos a través de análisis de curvas como las observadas en los diagramas Levy Jennings o cartas control.

Palabras clave: Incertidumbre, cromatografía de gases, CEIMA, calificación metrológica.

Introducción

Dentro de los parámetros que comúnmente aparecían en la incertidumbre se encuentran aquellos que generan la variabilidad más representativa. Generalmente estos parámetros se determinan de estudios que generan ponderaciones de las variabilidades, conocido como presupuesto de la incertidumbre (Le Maître y Knio, 2010). Considera importante tener una cantidad robusta de datos que sea funciones de densidad de probabilidad de tipo paramétrico, como lo vemos en la guía de incertidumbre, GUM (JCGM, 2008), que en nuestro país se ha condensado por la normatividad NMX-CH-140-IMNC-2002 (Instituto Mexicano de Normalización y Certificación, A.C., 2003). Las distribuciones de probabilidad descritas en dicha normatividad son de carácter paramétrico, cuya descripción de las probabilidades obedecen a las densidades clasificadas como normales: la propia distribución normal, la distribución rectangular o uniformes, triangular, densidades tipo t-student, entre las más usadas. Su amplia gama de áreas de aplicación va desde los procesos que atienden los laboratorios clínicos, de alimentos o de ensayos y calibración, demandando en cada una de estas áreas el cumplimiento de la robustes finalmente son normatividades demandas por referencias internacionales tales como las ISO 15189, ISO 22000, ISO 17025, entre otras que incluyen el cálculo de la incertidumbre, tal como lo demanda la guía del cálculo de la incertidumbre. Por otro lado, los laboratorios de cromatografía acreditados son laboratorios de análisis que cuentan con equipos cromatográficos necesario mantener la trazabilidad de las mediciones para desarrollar patrones de referencia y asegurar la certeza y exactitud de los resultados. La cadena ininterrumpida de mediciones desde el Sistema Internacional de Unidades a los valores medidos por el laboratorio que utiliza los patrones o instrumento patrón, demandados por las acreditadoras, se logran mediante el análisis de realizado mediante el uso de la ley de propagación de errores (Wei, Valdebenito, & Beer, 2021) o la demanda realizada por la guía para la estimación de la incertidumbre. Una vez que se pondera las posibles variables, que influyen en las mediciones, se determina la contribución que cada una de ellas en suman a la variabilidad total del proceso, también conocido como la determinación del presupuesto de la incertidumbre. De tal suerte que la incertidumbre de las mediciones, en casi todos los procesos científicos y tecnológicos, se han convertido en referentes para analizar otros aspectos que garanticen la calidad de las mediciones, anticipen posibles desviaciones y acompañen la toma de decisiones. Regulaciones de esta naturaleza las encontramos poco a poco como parte de la exigencia en la optimización de los recursos materiales, disminución de tiempos y la prevención como estrategia de ganar en el mercado (Vâlcu y Călin, 2018). De esta forma vemos que dos metodologías, que están presente alrededor de varios procesos, incluyendo aquellas como el caso de la cromatografía, son los métodos CEIMA y Calificación Metrológica (CM) (Khatmullina et al., 2021).

Las fuentes de incertidumbre de una medición más generales contemplan:

• Errores de apreciación del operador en la lectura de instrumentos analógicos.
• Resolución infinita del instrumento o umbral de discriminación finito.
• Valores inexactos de patrones de medición y materiales de referencia.
• Aproximaciones y suposiciones incorporadas en los métodos y procedimiento de medición.
• Variaciones en observaciones repetidas del mensurando bajo condiciones aparentemente iguales.
• Reactivos.
• Fuentes de incertidumbre asociadas con las mediciones.

Estas fuentes no son necesariamente independientes y, por supuesto, un efecto sistemático no reconocido no puede considerarse en la evaluación de la incertidumbre del resultado de una medición, pero contribuye a su error.
En el caso específico de los equipos cromatográficos, en los procesos de verificación y validación podemos determinar la comprobación de las siguientes variables, las cuales pueden corregirse mediante la calibración frecuente de los instrumentos:

En el sistema de dispensación

• Exactitud de la velocidad de flujo (HPLC).
• Exactitud de la velocidad de flujo (UHP
• Precisión de la velocidad de flujo.
• Exactitud de la composición del gradiente.
En el sistema de inyección

• Precisión de Volumen.
En el muestreador

• Exactitud para la temperatura.
• Compartimento de columna.
• Exactitud.
• Estabilidad.
En el detector de la onda variable

• Linealidad.
• Exactitud. para la longitud de onda.
• Ruido.
• Deriva (Drift).

Este último parámetro es uno de los que resultan altamente demandados en la determinación de variabilidades, pero que debido a los aspectos geométricos que representan pocas veces se incluye dentro del cálculo incertidumbre, lo que representa la posibilidad de obtener observaciones sobre las tendencias del incremento de variabilidad a lo largo del tiempo, llevando a la pérdida de credibilidad de las mediciones, un sistema poco operativo, inversión en el remplazo de componentes, pérdida de capacidad sobre la conformidad entre otras. Debido a la importancia de la evaluación del DRIFT se plantea el análisis para obtención del mismo mediante el uso de la traslación geometría, haciendo uso de las matrices de rotación, de los resultados de variabilidad y la obtención de las ecuaciones que definan la variable DRIFT, que puede ser obtenido por cualquier método de interpolación como lo es el caso del uso del método de mínimos cuadrados, pero que no es privativo de poder realizar una aproximación por otra metodología, siempre y cuando sea respaldado sin caer en de extrapolaciones.

Objetivo

El objetivo de esta investigación es calcular la variable del Drift de un proceso de medición realizado con un cromatógrafo utilizando el cambio geométrico de la matriz de rotación utilizando el traslado de ejes de simetría para la valoración del proceso de interpolación.

Materiales y métodos

Recordemos que de manera lineal:

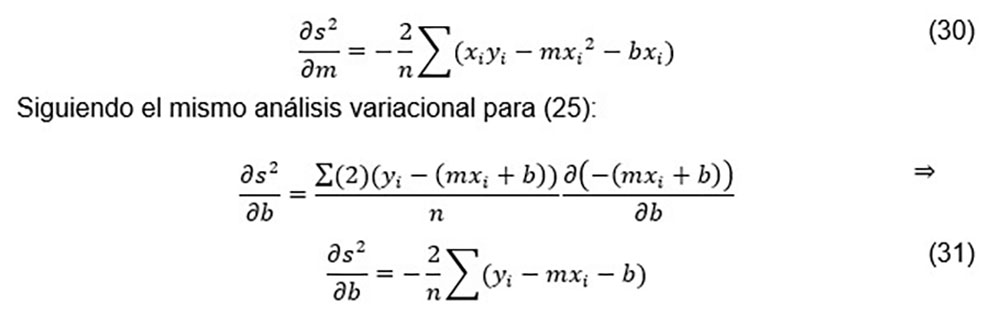
Discusión

Como se ha comentado al inicio de este ejercicio de investigación, los elementos de desarrollo acerca del DRIFT poco se ha estudiado, debido a las complicaciones de desarrollo que ello implica, sin que ello haya dejado de ser una necesidad a nivel internacional, como lo muestran estudios del arte al respecto. Las aproximaciones en su gran mayoría son de carácter numérico, por lo que los resultados presentados puede ser un elemento de partida para la evaluación de esta importante variabilidad en magnitudes como la cromatografía.

Conclusiones

La proyección del comportamiento del DRIFT, lo que en el espacio cartesiano y estadístico requiere de dar un tratamiento estadístico que es complicado al mantener una inclinación sobre la horizontal, por lo que dentro de la metodología seguida se encontraron las matrices de rotación, que, combinada con el método de mínimos cuadrados, nos ha permitido dar cabal cumplimiento al objetivo planteado, pudiendo encontrar las siguientes observaciones:
a) Para el caso lineal, se genera una expresión, ecuación (19) con condiciones de rotación para poder analizar el DRIFT.
b) El uso de la regla de la cadena, ampliamente usada en cálculo diferencial, ecuaciones (26) y (27) han dado lugar al tratamiento de un sistema óptimo para el manejo de los datos cuando tienen condiciones espaciales, inclinadas como el caso del DRIFT.
c) Al solucionar el sistema de ecuaciones tenemos los valores de m y b como:

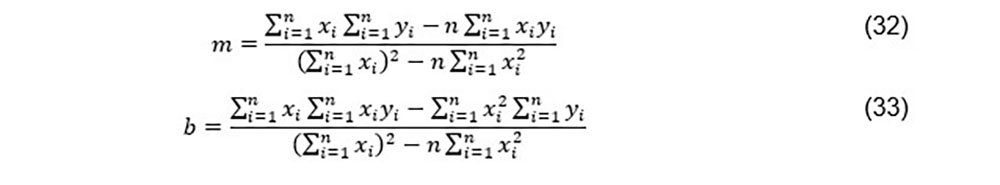
Referencias

• Instituto Mexicano de Normalización y Certificación, A.C. (2003). NMX-CH-140-IMNC-2002. Guía para la expresión de incertidumbre en las mediciones.
• JCGM. (2008). GUM. Evaluation of measurement data — Guide to the expression of uncertainty in measurement. 100.
• Khatmullina, R., Shutkova, D., & Vaks, M. (2021). Current State of Standardization in the Field of Metrological Support of Information and Measurement Systems. Norwegian Journal of Development of the International Science, (64): 75-77.
• Le Maître, O.P., & Knio, O.M. (2010). Introduction: Uncertainty quantification and propagation. Spectral methods for uncertainty quantification, 1-13.
• Vâlcu, A., & Călin, A. (2018). Asegurar la validez de los resultados mediante comprobaciones intermedias en el campo de las mediciones de masa. Journal of Physics: Conference Series, 1065(4): 042033.
• Wei, P.L., Valdebenito, M., & Beer, M. (2021). Bayesian probabilistic propagation of imprecise probabilities with large epistemic uncertainty. Mechanical Systems and Signal Processing, 149: 107219.

Quinto Congreso Nacional de Tecnología 19, 20 y 21 de octubre de 2022,
celebrado en formato virtual

---

Excepto donde se indique lo contrario esta obra está bajo una licencia Creative Commons Atribución No comercial, No derivada, 4.0 Internacional (CC BY NC ND 4.0 INTERNACIONAL).
https://creativecommons.org/licenses/by-nc-nd/4.0/deed.es

FORMA SUGERIDA DE CITAR:

Estevez-Delgado, G., Estevez-Delgado, J., y Palomares-Rizo, V. B. (2022). Una propuesta de las matrices de rotación para el manejo del drift. MEMORIAS DEL CONGRESO NACIONAL DE TECNOLOGÍA (CONATEC), Año 5, No. 5, septiembre 2022 - agosto 2023. Facultad de Estudios Superiores Cuautitlán. UNAM. https://tecnicosacademicos.cuautitlan.unam.mx/CongresoTA/memorias2022/mem2022_ExtensoPaper4.html

---