Inicio / Archivo / Año 6, No 6, septiembre 2023 - agosto 2024 / Paper 23

---

DESARROLLO DE UN PROGRAMA PARA LA CONSTRUCCIÓN DE
DZP USANDO MATLAB

Eduardo Iván Pérez-Gómez, Adrián Ricardo Hipólito-Nájera^*, María del Rosario Moya-Hernández, Norma Rodríguez-Laguna, Juan Carlos Rueda-Jackson y Rodolfo Gómez-Balderas
Laboratorio de Fisicoquímica Analítica, UIM, FES Cuautitlán
*ricardohipolito@cuautitlan.unam.mx

Resumen

El estudio del equilibrio termodinámico de sistemas multicomponentes y multirreaccionantes sigue siendo en la actualidad un modelo útil para determinar la estabilidad y el comportamiento químico general de las diferentes especies presentes en él mismo. Con el fin de establecer de manera rápida las condiciones de equilibrio del sistema, así como de predecir las reacciones que ocurren en él, se ha propuesto la aplicación de métodos gráficos que incluyen diagramas de distribución y logarítmicos, así como diagramas de zonas de predominio (DZP). Para facilitar los cálculos involucrados para los DZP es posible usar programas computacionales. El programa elegido en este trabajo es MATLAB, ya que presenta un lenguaje y una interfaz amigable, para la programación de la matemática involucrada en la química. Además, MATLAB tiene la posibilidad de crear aplicaciones sin la necesidad de programas adicionales. En este trabajo se compilaron las ecuaciones necesarias y se desarrolló un programa para el cálculo y la construcción de DZP en 2D con MATLAB. Con el programa creado, fue posible construir diagramas de sistemas químicos en donde una sola molécula de M reacciona con una sola molécula de L, pero de manera simultánea M reacciona con OH^– y L reacciona con H⁺, así como el complejo ML pueda presentar reacciones con OH^– o H⁺. El programa crea diagramas que pueden ser comparados con los reportados en la literatura.

Palabras clave: Diagramas de zonas de predominio, constantes condicionales, programación, química analítica, método de Ringbom.

Introducción

El estudio de procesos que involucran especies en solución requiere de un conocimiento preciso de la estabilidad de las diferentes especies químicas existentes en cada una de las fases presentes en el sistema a considerar, así como la coexistencia de estas diferentes fases. El estudio del equilibrio termodinámico de sistemas multicomponentes y multirreaccionantes sigue siendo en la actualidad un modelo útil para determinar la estabilidad y el comportamiento químico general de las diferentes especies presentes en el mismo (Rojas, 1992; Rojas, 1995a). Cuando el número de las especies y/o reacciones químicas es grande, casi siempre es necesario utilizar métodos iterativos para determinar la composición de equilibrio termodinámico del sistema (Rojas, 1995b). Con el fin de establecer de manera rápida las condiciones de equilibrio del sistema, así como de predecir las reacciones que ocurren en él, se ha propuesto la aplicación de métodos gráficos que incluyen diagramas de distribución y logarítmicos, así como Diagramas de Zonas de Predominio (DZP) (Rojas, 1995b,c). El método de Ringbom muestra que es posible realizar un estudio de más de dos componentes mediante la generalización de leyes de acción de masas (constantes de equilibro condicionales) que, si es el caso, incorporan la presencia de agentes a concentraciones altas y constantes (amortiguados), manteniendo ecuaciones análogas a la de sistemas de sólo dos componentes (Ringbom, 1979).

Con objeto de aclarar la naturaleza de la constante condicional, consideraremos la reacción de complejación.

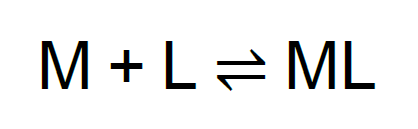
El equilibrio de la reacción antes indicada puede definirse mediante la expresión:

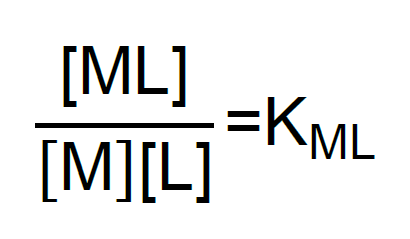
donde K_ML es la constante de formación.

Con objeto de conservar la ecuación de equilibrio en una forma sencilla, en forma de una constante condicional (K’) sería:

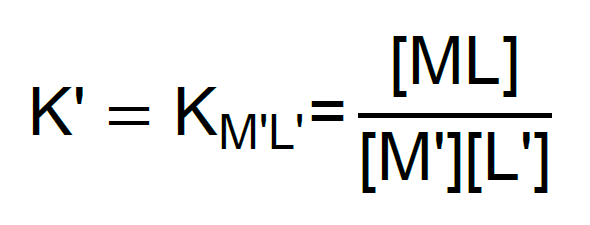
En esta expresión [M’] indica la concentración no sólo del ion metálico libre, sino también de todas las especies posibles del metal en solución que no ha reaccionado con el agente complejante. Por su parte, [L’] representa no sólo la concentración del ligando libre, sino también la de todas las especies del agente complejante no unidas al metal.

Si usamos fracciones que constituyen medidas del grado en que se producen reacciones simultáneas, podemos definir para M y L:

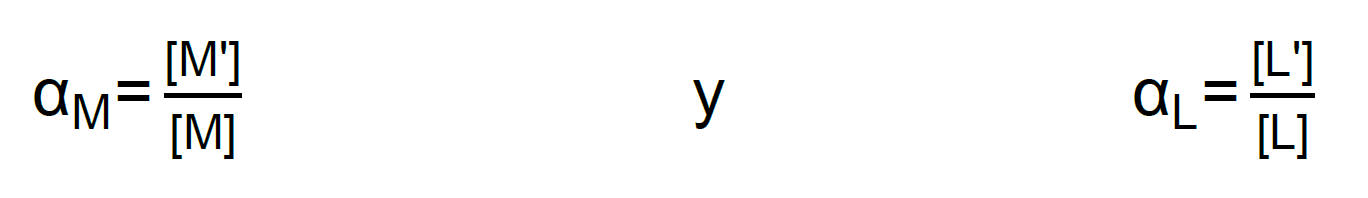
Sustituyendo en K’, se obtiene:

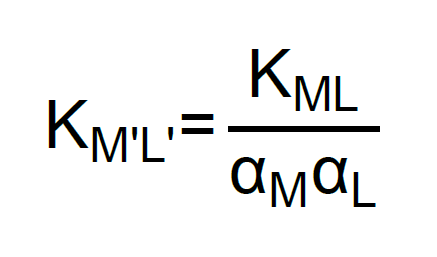
En este sentido, si además de la ecuación , M también reacciona con A se definiría una ecuación como y se definiría la siguiente fracción:

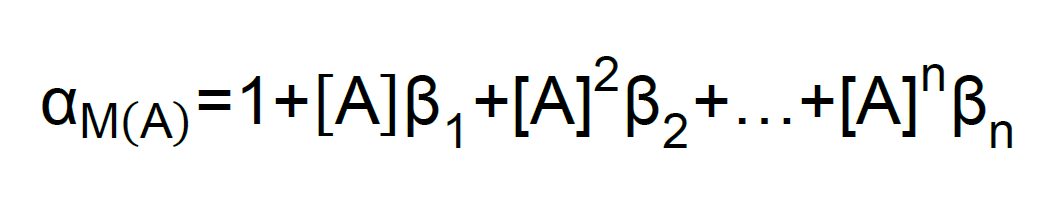
donde:

β es la constante de formación global, el subíndice indica el número de moléculas de A que reaccionarán con M, desde 1 hasta n.

Asimismo, además de la ecuación , L reacciona al mismo tiempo con B con su ecuación se definiría una nueva fracción.

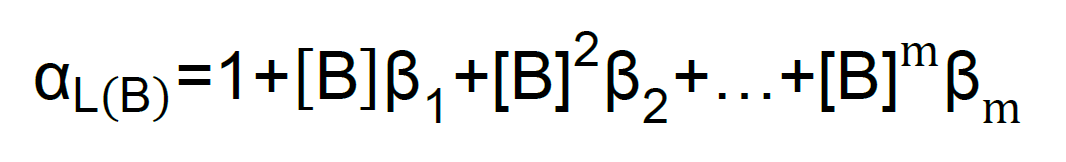
donde:

β es la constante de formación global, el subíndice indica el número de moléculas de B que reaccionarán con M, desde 1 hasta m.

Estos cálculos pueden realizarse a mano, pero suelen ser difíciles de manejar por su extensión, con posibilidad de cometer errores humanos. Por lo que es necesario usar un método en el que se pueda generalizar y facilitar el cálculo. Para que sólo sea necesario cambiar pocas variables como las constantes de complejación K_ML o las β, según sea el caso. Estos cálculos pueden facilitarse con la ayuda de programas de computadora (Rojas, 1995a).

Se conocen muchos programas de computadora que pueden ayudar a facilitar el procesamiento de datos. En este trabajo, se hace uso del programa MATLAB (MATrix LABoratory), que como lo dice su nombre, trabaja principalmente con matrices de datos, usando el lenguaje M, el cual es propio del programa (Eugeniy, 2018; Eshkabilov, 2019). El lenguaje no es difícil de utilizar y es muy amigable para poder visualizar funciones y gráficos en 2D. Además, en años recientes, las prestaciones de este programa, han llegado a tal punto de poder crear aplicaciones o programas para tareas particulares (Eugeniy, 2018). Existen muchas aplicaciones de MATLAB enfocadas a la química (Maeder, 2007). Sin embargo, hasta el momento no existe un programa en este lenguaje en el que se puedan construir gráficos en 2D del valor de K’ en función de una especie amortiguada M, L, A, B, etc.

Objetivo

Compilar las ecuaciones necesarias para el cálculo y la construcción de DZP en 2D con MATLAB para posteriormente desarrollar un programa.

Materiales y métodos

Computadora con el programa MATLAB versión R2023a. Con herramienta de diseño de aplicaciones de MATLAB, con los siguientes componentes

Sistema operativo:

Windows: Windows 11.

Mac: macOS Big Sur, version 11.7.6

Procesador: Intel o AMD x86-64 con soporte de instrucciones AVX2

Disco: 2 GB solo para MATLAB, 4-6 GB para una instalación típica.

RAM: 1GB mínimo, 4 GB recomendado.

Tarjeta gráfica: Soporte para OpenGL 3.3 recomendado con 1 GB en GPU.

El método de construcción de los diagramas es el descrito por Ringbom utilizando los datos de constantes por este mismo autor (Ringbom, 1979).

Resultados

A continuación, se muestran los resultados del programa obtenido en la Figura 1 a 3, mostrando las ventanas más relevantes que se describirán más a fondo en la sección siguiente.

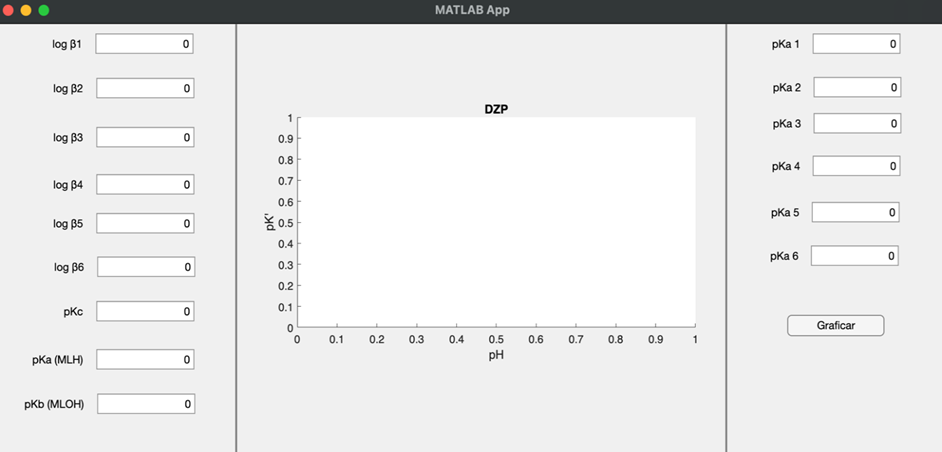
Figura 1. Ventana principal del programa, se muestran las 3 columnas que lo conforman.

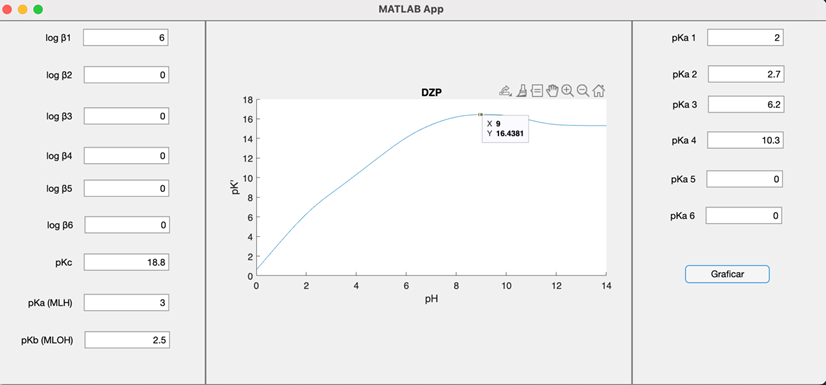
Figura 2. Sistema Cu-EDTA a diferentes valores de pH. Los valores de constantes de equilibrio utilizadas se muestran en su casilla correspondiente. El cursor muestra que a pH = 9 pK’ = 16.4381.

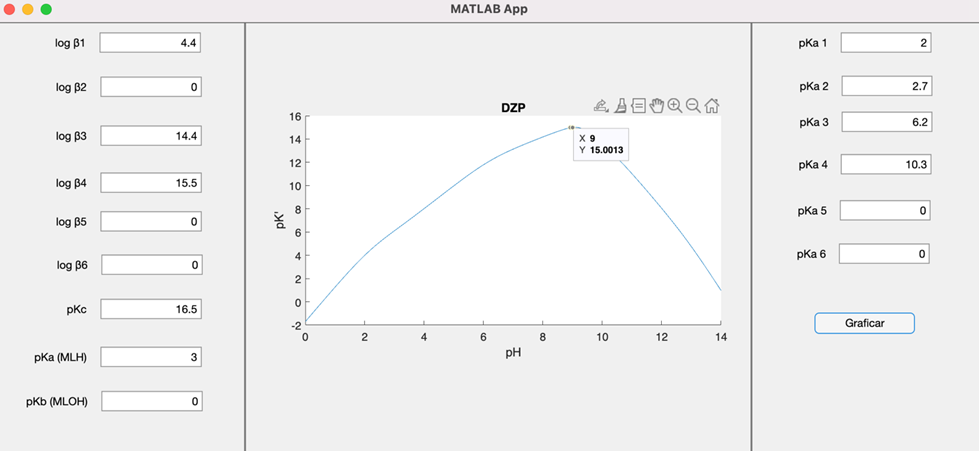
Figura 3. Sistema Zn-EDTA a diferentes valores de pH. Los valores de constantes de equilibrio utilizadas se muestran en su casilla correspondiente. El cursor muestra que a pH = 9 pK’ = 15.0013.

El programa funciona sólo para sistemas en donde está involucrado una sola molécula de M que reacciona con una sola molécula de L, pero de manera simultánea M reacciona con OH^– y L reacciona con H⁺, así como el complejo ML pueda presentar reacciones con OH^– o H⁺.

Discusión

Las ecuaciones presentadas en la sección de introducción fueron compiladas dentro del programa, con el lenguaje apropiado, por simplifación no se muestran. Estas ecuaciones fueron posteriormente compiladas dentro de la herramienta de diseño de aplicaciones de MATLAB, usando plantillas preestablecidas. La ventana de inicio del programa se muestra en la Figura 1. Se divide en tres columnas, en la primera, se colocan los valores de las constantes de complejación (β) de M con el ion hidróxido (OH^–), más abajo se puede escribir la constante de complejación (pK_c) de M con L, más abajo se encuentra un espacio para escribir las constantes de formación, del complejo ML que forma complejos con ion hidrónio (H⁺) (pK_a (MLH)), en el último espacio debe escribirse la constante de formación de ML con OH^– (pK_b (MLOH)). En la columna siguiente, se muestra el gráfico del –logK’ = pK’ contra el –log[H⁺] = pH, por último, en la 3er columna deben escribirse las constantes de formación sucesivas de L con H⁺ que suelen llamarse pK_a. Por último, se tiene el botón de graficar. Debe señalarse que si no se tiene algún valor de constante debe escribirse 0. Una vez que se han colocado los valores debe presionarse el botón de graficar. En la columna de en medio se mostrará el gráfico deseado. En la Figura 2 se muestra el gráfico del sistema M = cobre (Cu) y L = ácido etilendiaminotetraacético (EDTA). Con el cursor es posible conocer el valor de pK’ en algún valor de pH, al posicionarse sobre el gráfico.

En la Figura 3 es posible ver un ejemplo más para el sistema de zinc (Zn) con EDTA, en este ejemplo se tienen las constantes globales de formación con OH^–, de las cuales, sólo se tiene el valor de logβ₁, la logβ₃ y la logβ₄. El no tener la constante logβ₂ (que indica que no hay valores reportados para este complejo Zn(OH)₂) no produce errores en el programa y puede, de igual manera, realizar el gráfico correspondiente. En este ejemplo, tampoco se tiene el valor de pK_b (MLOH) y de igual manera el programa funciona de manera adecuada, además de que los gráficos realizados coinciden con los reportados por Ringbom. Aunque, hasta el momento, se pueden realizar sólo diagramas para sistemas en donde está involucrado una sola molécula de M que reacciona con una sola molécula de L, se sigue realizando la compilación de las ecuaciones necesarias para poder involucrar reacciones en donde puedan reaccionar más de una molécula de M y L.

El programa puede ser descargado accediendo a la carpeta que contiene el programa de instalación usando el código QR de la Figura 4, se debe contar con el programa MATLAB 2023a instalado.

Figura 4. Código QR para el acceso a la carpeta contenedora.

Conclusiones

Fue posible realizar la compilación de las ecuaciones responsables para la construcción de los DZP, según la metodología de Ringbom, en el programa MATLAB. Se logró desarrollar un programa para la construcción del DZP usando la plataforma de MATLAB y puede ser utilizado por cualquier usuario familiarizado con la metodología de Ringbom y con el uso de MATLAB.

Agradecimientos

Los autores agradecemos a los siguientes programas: UNAM-PAPIIT IA208221, IN221621 and IA209123 de la Dirección General de Asuntos del Personal Académico, proyecto PIAPI2035 y Programa de Cátedras de Investigación CI2220 de la FES-Cuautitlán, UNAM. UNAM-PAPIME PE209023, PAPIIT IA202122.

Referencias

Eshkabilov, S. (2019). Beginning MATLAB and simulink: From novice to professional. In Beginning MATLAB and Simulink: From Novice to Professional. https://doi.org/10.1007/978-1-4842-5061-7

Eugeniy, E. M. (2018). Programming with MATLAB for Scientists. In Programming with MATLAB for Scientists. https://doi.org/10.1201/9781351228183

Jiménez, A. Y. A. (2011). Material didáctico para la asignatura de Química Analítica Aplicada de las Licenciaturas en Farmacia y Bioquímica Diagnóstica.Tesis. UNAM.

Maeder, M., & Neuhold, Y. M. (2007). Practical data analysis in chemistry. 326.

Ringbom, A., & Montuenga, C. (1979). Formación de complejos en química analítica (C. Montuenga, Ed.). Alhambra.

Rojas, H. A. (1995a). El método de especies y equilibrios generalizados para el estudio de sistemas químicos en equilibrio bajo condiciones de amortiguamiento: teoría y algoritmos de los Diagramas de zonas de predominio. Tesis. UAM.

Rojas, H. A., Ramirez, M. T., & González, I. (1995b). Predominance-Zone Diagrams in Solution Chemistry. Journal of Chemical Education, 72(12), 1099-1105.

Rojas, H. A., Ramírez, M. T., González, I., & Ibáñez, J. G. (1995c). Predominance-zone diagrams in solution chemistry: Dismutation processes in two-component systems (M-L). Journal of Chemical Education, 72(12), 1099–1105. https://doi.org/10.1021/ed072p1099

Rojas, H. A., Ramírez, M. T., González, I., & Ibáñez, J. G. (1992). Multi-dimensional predominance-zone diagrams for polynuclear chemical species. Analytica Chimica Acta, 259(1), 95–104. https://doi.org/10.1016/0003-2670(92)85080-P

Sexto Congreso Nacional de Tecnología 18, 19 y 20 de octubre de 2023,
celebrado en formato virtual

---

Excepto donde se indique lo contrario esta obra está bajo una licencia Creative Commons Atribución No comercial, No derivada, 4.0 Internacional (CC BY NC ND 4.0 INTERNACIONAL).
https://creativecommons.org/licenses/by-nc-nd/4.0/deed.es

FORMA SUGERIDA DE CITAR:

Pérez-Gómez, E. I., Hipólito-Nájera, A. R., Moya-Hernández, M. R., Rodríguez-Laguna, N. L., Rueda-Jackson, J. C., y Gómez-Balderas, R. (2023). Desarrollo de un programa para la construcción de DZP usando MATLAB. MEMORIAS DEL CONGRESO NACIONAL DE TECNOLOGÍA (CONATEC), Año 6, No. 6, septiembre 2023 - agosto 2024. Facultad de Estudios Superiores Cuautitlán. UNAM. https://tecnicosacademicos.cuautitlan.unam.mx/CongresoTA/memorias2023/Mem2023_Paper23-EC.html