OBTENCIÓN DE LOS PERIODOS DE CALIBRACIÓN MEDIANTE LA
CONVOLUCIÓN A LA DERIVA INSTRUMENTAL

Gabino Estevez-Delgado¹, Joaquin Estevez-Delgado², Edgar Samuel Lara-Murillo¹ y Paulina Ponce-Ávila^1
1Universidad Michoacana de San Nicolás de Hidalgo. Facultad de Químico Farmacobiología. ²Universidad Michoacana de San Nicolás de Hidalgo. Facultad de Ciencias Físico Matemáticas
*gabino.estevez@umich.mx

Resumen

Dentro de la estructura metrológica que demandan las empresas, para tener resultados confiables y de alta, se encuentran dos características de interés particular como lo son la homogeneidad y homocedasticidad en las mediciones. Siendo este último un factor clave para buscar una variabilidad mínima que nos llevara a tener mejor calidad en las mediciones, al ser el concepto de la calidad una función inversa de la variación total. Como resulta natural, el concepto de la variabilidad y de la calidad involucran conceptos como la repetibilidad y la reproducibilidad, como conceptos canónicos de la ciencia y la tecnología, es decir, la posibilidad de poder ser observado el mismo fenómeno ante condiciones iguales. Dentro del esquema metrológico el BIPM y la organización ISO, han generado una estructura dentro de la metrología legal para poder garantizar la reproducibilidad, con calidad mediante la trazabilidad que se otorga como parte del proceso de heredar mediante la calibración propiedades de variabilidad mínima llamada incertidumbre. Sin embargo, este proceso representa un gasto para las empresas, en las que, en muchas ocasiones, sí existen guías técnicas, que independiente del uso de los instrumentos, se dictan cuándo se debe realizar una calibración; en tanto que, en otros casos no existe estimación puntual de cuando llevar a cabo una calibración, lo que puede generar gastos excesivos para las empresas que trabajan con estándares de calidad acreditados. En este sentido, se ha observado que realizar calibraciones por varios periodos con un mismo proveedor permite realizar análisis apropiados sobre los tiempos de calibración. El presente trabajo ofrece la posibilidad de extender los periodos de calibración a través de las verificaciones intermedias al considerar posibles variaciones dadas en la deriva instrumental, particularmente el caso de termómetros, cuyo análisis se realiza mediante la aplicación de una función de convolución.

Palabras clave: Tolerancia, perturbación, variabilidad, deterioro instrumental.

Introducción

El proceso de calibración de instrumentos de medición obedece a una serie de cumplimientos, tanto de carácter legal como científico. Por un lado, los organismos reguladores de la conformidad, como lo son los organismos acreditadores de regulaciones internacionales, demandan dar cumplimiento de requisitos que las empresas adquieren cuando declaran que la calidad de sus procesos a través de un estándar internacional o nacional. En otro sentido, la adopción de regulaciones compromete a las empresas mantener esquemas de comparación de resultados entre pares, no solo de empresas de su país sino de cualquier parte del mundo que trabaja con la misma regulación. Ambas condiciones demandan comparaciones de los procesos realizados, no solo de carácter normativo sino del cumplimiento científico a través de una serie de teoremas como lo es el teorema de límite central que nos asegura que presentamos la información suficiente cuando los procesos están finamente equiparable para ser comparados (Damasceno y Couto, 2018).

La estructura metrológica, dentro de los aspectos legales, exigen normatividades que permiten la reproducibilidad de los fenómenos (Tetens, 2016). Esa reproducibilidad exige que los fenómenos tengan variabilidades mínimas, lo que para lograrlo demanda mantener las condiciones similares para la replicación de los resultados.

Como parte de la formalidad de las mediciones realizadas, se observa que una buena determinación de las condiciones ambientales, de las instalaciones donde se realiza la medición, del personal adecuado y muy puntualmente de la determinación de la cantidad de datos que se miden como parte de la repetibilidad o de la reproducibilidad son claves para poder realizar comparaciones entre dos mediciones sobre el mismo fenómeno.

Dentro de la estructura de normalización, es de interés particular el tratamiento que se le da a la información obtenida partiendo sobre el criterio de tener información suficiente para generar análisis estadístico con distribuciones de carácter paramétrico. Es precisamente este punto de partida que dan origen a una serie de observaciones que permiten garantizar la calidad de las mediciones, construyendo métodos desde el propio diseño de experimentos, las instalaciones de los laboratorios o empresas, el manejo de las condiciones ambientales que generaran los mejores resultados, el remplazo de instrumentos, la capacitación del personal, el uso de periféricos y auxiliares para garantizar la calidad, impactando también la contratación de servicios y cuidado de la materia prima que intervienen en los productos finales.

Particularmente, en el campo de la metrología científica, se parte de un criterio principal que se empara con el teorema de límite central, que se fundamenta en la función normal o gaussiana (1), que es la emisión de dos resultados como lo son los errores de medición y la variabilidad, (𝜇,𝜎²).

Dentro del esquema de comparación internacional, se emite un documento como producto de todas las mediciones que realizan los laboratorios de ensayo y calibración de acuerdo con el estándar ISO 17025 conocido como certificado de calibración (Anastasopoulos, 2017), que contiene la información mínima suficiente como son el error e incertidumbre de medida (∈,𝑈). Este busca garantizar que, además de haberse realizado las mediciones en condiciones de reproducibilidad, estas sean estrictamente equiparables con otros laboratorios que han cuidado sus instalaciones, el método, los instrumentos, el personal y los materiales.

Sin embargo, una de las consideraciones más importantes para los laboratorios de ensayos o calibraciones parte de la construcción epistémica en la que las mediciones son trazables al sistema internacional de unidades a través de la trazabilidad (Damasceno y Couto, 2018), considerando que, todo lo que en ella interviene son de carácter normal y no solo el proceso de repetibilidad, es decir, los instrumentos utilizados y reactivos son acompañados de funciones de densidad de probabilidad normal amparadas en su certificado de calibración y mantenidos a lo largo del tiempo (JCGM, 2008).

Dentro del análisis formal que garantizan dentro de la metrología el teorema de límite central, para el caso de la variabilidad se encuentra la ley de propagación de errores, en las que se consideran todas las posibles fuentes de incertidumbre que provocan variaciones en las mediciones, como lo son las características propias de los equipos y materiales y la variabilidad que generan el personal que realiza las mediciones (Kellner y Ceriotti, 2024). La ley de propagación de errores permite la obtención de incertidumbre que representa todas contribuciones, de aquellas fuentes de incertidumbre más significativas, de la forma

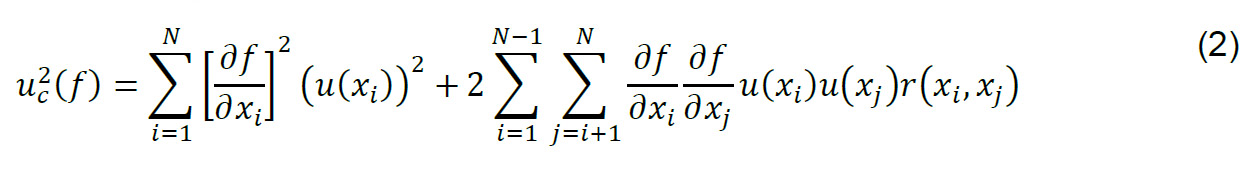
Donde 𝑢(𝑥_𝑖) son las incertidumbres asociadas a las características del instrumento y de la medición, 𝑓 es la función del modelo físico asociado a fenómeno a medir, dependientes de las variables independientes 𝑥_𝑖 y 𝑟(𝑥_𝑖,𝑥_𝑗) y el coeficiente correlación de Pearson, de ser significativa la correlación entre las variables.

Esta expresión suele expresarse de la forma:

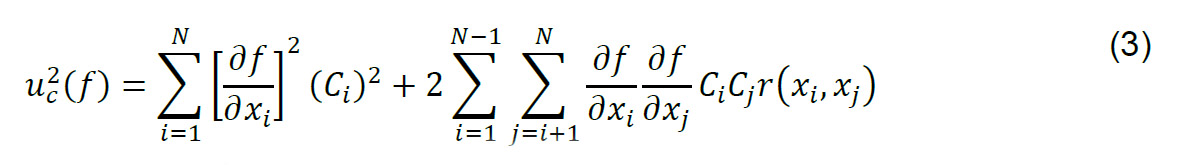
Donde, 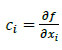son los coeficientes de sensibilidad para el modelo físico asociado a las mediciones. Cuando el modelo diseño experimental o las condiciones de medición lo permite, suele eliminarse las correlaciones entre las incertidumbres, para expresar la ecuación (3) de la forma:

Por otro lado, para obtener el factor de cobertura correspondiente, que señala el nivel de confianza dentro de una distribución normal, se obtiene de la ecuación siguiente, conocida como la incertidumbre expandida, que es la que es dada en los procesos de calibración en los certificados o informes de calibración (Demeyer et al., 2022):

Una de estas fuentes de incertidumbre, que forman parte de las variables de influencia en la estimación de la incertidumbre, es la deriva instrumental, la cual de manera natural se presenta en todos los instrumentos de medición debido al deterioro natural de los componentes físicos o químicos del instrumento (Cox y O’Hagan, 2022).

La función de densidad de probabilidad, asociada a la deriva instrumental, generalmente es una distribución rectangular dada como:

La cual, en otras ocasiones, cuando el deterioro es acelerado, pudiera ser considerada como una función exponencial de la forma:

Sea cualquiera de estas dos últimas ecuaciones, el comportamiento de la deriva se debe de considerar que existen recomendaciones emitidas en guías técnicas como la norma ILAC – G24 Directrices para la Determinación de los Periodos de Calibración de los Instrumentos de Medición, (INTERNATIONALE, 2008), promovidos por organismos de reconocimiento internacional, como lo es la Organización Internacional de Metrología Legal (OIML), que contemplan un análisis general para los instrumentos de medición pero que están sujetos a las condiciones de operación, comúnmente denominadas condiciones del laboratorio (Carbone et al., 2001).

La guía ILAC–G24 diferencia 5 formas en las que se puede realizar recomendaciones para poder determinar los periodos de calibración de un instrumento, de manera particular nos interesa aquella en la que el uso de la incertidumbre nos remonta al uso adecuado del teorema de límite central (Bianchi y Secco, 2021) y la ley de grandes números, como la parte más rigurosa de la obtención de periodos confiables, llamado Ajuste automático o “Escalera” (tiempo-calendario).

Para la metodología ajuste automático se requiere contextualizar que el cálculo de los periodos de calibración requiere la determinación de otro parámetro adicional al concepto de la deriva llamado tolerancia, que corresponde a la variabilidad máxima en una región, de tal forma que el periodo de calibración esta dado como:

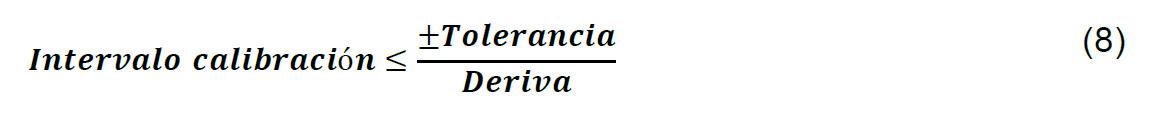
donde la deriva se calcula como:

Otra de las metodologías dadas como recomendación son aquellas en la que se monitorea la desviación que alcanza el error máximo permisible, ya que es en ese punto en el que se considera el intervalo de calibración. El intervalo de calibración es dado también por la ecuación (8), sin embargo, la deriva suele expresarse en función de las horas de uso del instrumento y expresada como:

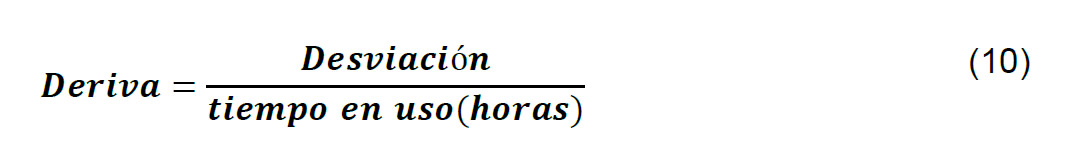
Si bien existen condiciones para la ponderación de los periodos de calibración expresados en función de la correlación que se tiene de las incertidumbres a lo largo del tiempo (Estevez y Estevez, 2021), estas pueden ser limitativas ante variaciones no perceptibles en el reporte de los certificados de calibración y que pudieran abordarse si se pueden calcular pequeñas variaciones que modifican la condición la función de densidad rectangular asociada a la deriva instrumental (Velychko y Gordiyenko, 2019).

Objetivo

Determinar cómo son las aportaciones de la deriva instrumental cuando se consideran valores de perturbación lineal mediante el método de la convolución.

Materiales y métodos

Se conoce que cuando los intervalos de calibración en las que las variaciones máximas son dadas por un mismo proveedor de los servicios de calibración podemos considerar a la deriva instrumental potencialmente dada como:

Para el caso de variaciones con carácter lineal

El valor de la deriva sería del tamaño de la pendiente de la curva interpolada lo que permitiría expresar los periodos de calibración directamente como:

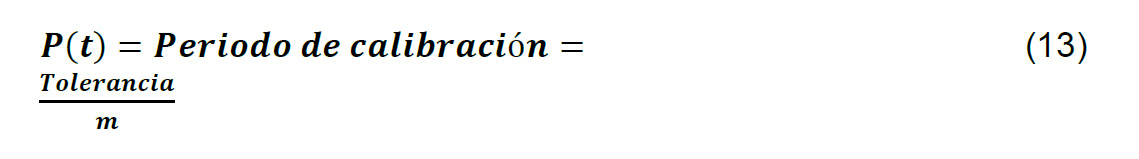
Y considerando calibraciones para un termohigrómetro, considerando sus errores de medida como los presentados en la tabla 1, en la escala de las temperaturas (Ekici y Avci, An International Bilateral Inter-Laboratory Temperature Comparison Measurement, 2023), con tolerancia de 0.03, del reporte de las mediciones consecutivas dadas como:

Tabla 1. De errores obtenidos de certificados de calibración por tres años consecutivos.

---

AÑO	Valores de referencia 0.94
2018	0.05
2019	0.07
2020	0.08

---

Nota. Una vez que se realiza el proceso de interpolación se obtiene una linealidad positiva, con r=0.9820, y una pendiente de 0.015.

Haciendo uso de la ecuación (13) se obtiene un periodo de calibración de 2 años. Sin embargo, el uso de considerar una perturbación mediante el uso de la convolución nos podría conducir a un mejor estimado metrológico.

Resultados

Recordando que los periodos de calibración, de (13), estos pueden ser considerados como una función de la forma:

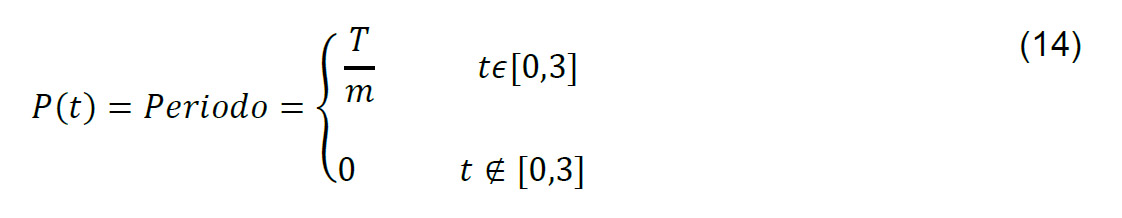
Donde es la tolerancia del instrumento y la pendiente de la curva de interpolación del histórico de incertidumbre de calibración reportados en los certificados de calibración.

Por otro lado, consideremos un impulso en el alcance de la función de trabajo o de operación de uso rutinario, de la forma:

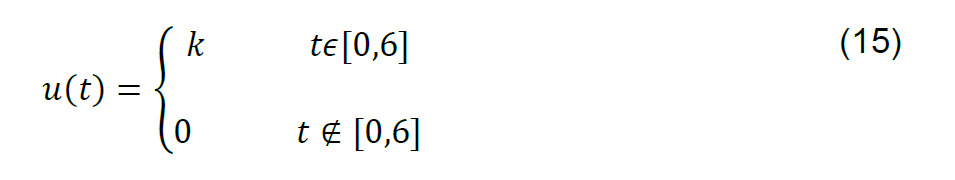
Así la función convolución con la que podremos determinar un impulso:

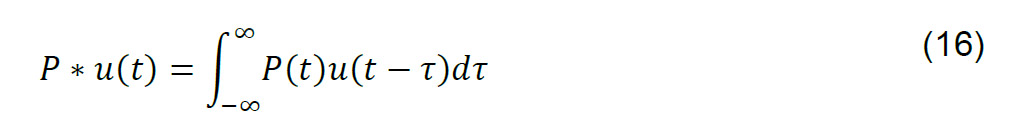
Lo que nos lleva a la función:

Nótese que el valor en el intervalo de un periodo de 0 a 3 años coincide con el cálculo de estimado para la ecuación (10) con k=1 y de acuerdo con este criterio no podrá exceder de un periodo mayor de 5 años, si se considera el último intervalo, estos exceden los valores ideales de uso de termómetro por que los valores generan expectativas poco realistas debido al deterioro del termopar que constituye la parte física del sensor de este tipo de instrumentos,

Discusión

Se observa que la perturbación que pueda generar alguna modificación del termopar que es común en los termómetros digitales, pueden modificar ligeramente el intervalo de los periodos de calibración, resultando rentable para periodos mayores a tres calibraciones consecutivas con intervalos regulares.

Conclusión

La interpolación presentada ha permitido validar que el análisis de convolución, en términos prácticos, es rentable si se mantiene adecuadamente el equipo, porque de haber un deterioro en los sensores el valor del impulso sería menor a k=1, lo que obligaría a una calibración anticipada.

Es importante destacar que, generalmente las mediciones de una medición al realizarse en condiciones controladas conllevan mantener un sistema trazable, pero que además puede aumentar los periodos de calibración y en consecuencia disminuir los gastos de calibración. De manera complementaria, se puede generar un estudio de repetibilidad y reproducibilidad del equipo y prueba del error normalizado a fin de darle soporte a la decisión de extender el periodo de calibración del equipo.

Agradecimientos

Agradecemos el apoyo de la Coordinación de Investigación Científica de la Universidad Michoacana de San Nicolás de Hidalgo.

Referencias

• Anastasopoulos, G. (2017). The new ISO/IEC 17025: 2017. CAL LAB the International Journal of Metrology, 30-35.
• Bianchi, D., Secco, N. (2021). Misconceptions about the Central Limit Theorem in Uncertainty-based Design Optimization. In AIAA Scitech 2021 Forum, 1594.
• Carbone, P., Macii, D., Petri, D. (2001). Measurement uncertainty and metrological confirmation in documented quality systems. In Proc. IMEKO TC4 Symposium, 2: (437-441).
• Cox, M., O’Hagan, A. (2022). Meaningful expression of uncertainty in measurement. Accreditation and Quality Assurance, 27(1): 19-37.
• Damasceno, J.C., Couto, P.R. (2018). Methods for evaluation of measurement uncertainty (Vol. 2). London, UK: IntechOpen.
• Demeyer, S., Fischer, N., Elster, C. (2022). Guidance on Bayesian uncertainty evaluation for a class of GUM measurement models. Metrologia, 58(1): 014001.
• Ekici, C., Avci, Ö. (2023). An International Bilateral Inter-Laboratory Temperature Comparison Measurement. MAPAN, 38(3): 569-572.
• Estevez, G., & Estevez, J. (2021). Periodos de calibración para instrumentos que mantienen una trazabilidad estática, una arista a la guía ILAC-G24 / OIML D 10. In C. d. Óptica. Trabajos Científicos en México, 6: 575-579.
• INTERNATIONALE, O. (2008). Guidance ILAC-G24 international OIML D 10.
• JCGM. (2008). GUM Evaluation of measurement data — Guide to the expression of uncertainty in measurement. 100:2008.
• Kellner, M., Ceriotti, M. (2024). Uncertainty quantification by direct propagation of shallow ensembles. Machine Learning: Science and Technology, 5(3). https://doi.org/10.1088/2632-2153/ad594a
• Tetens, H. (2016). Reproducibility, objectivity, invariance. Reproducibility: Principles, Problems, Practices, and Prospects, 13-20.
• Velychko, O., Gordiyenko, T. (2019). Metrological traceability at different measurement levels. In Standards, Methods and Solutions of Metrology. IntechOpen. IntechOpen.

Séptimo Congreso Nacional de Tecnología 16, 17 y 18 de octubre de 2024,
celebrado en formato virtual

---

Excepto donde se indique lo contrario esta obra está bajo una licencia Creative Commons Atribución No comercial, No derivada, 4.0 Internacional (CC BY NC ND 4.0 INTERNACIONAL).
https://creativecommons.org/licenses/by-nc-nd/4.0/deed.es

FORMA SUGERIDA DE CITAR:

Estevez-Delgado, G., Estevez-Delgado, J., Lara-Murillo, E. S., y Ponce-Ávila, P. (2024). OBTENCIÓN DE LOS PERIODOS DE CALIBRACIÓN MEDIANTE LA CONVOLUCIÓN A LA DERIVA INSTRUMENTAL. MEMORIAS DEL CONGRESO NACIONAL DE TECNOLOGÍA (CONATEC), Año 7, No. 7, septiembre 2024 - agosto 2025. Facultad de Estudios Superiores Cuautitlán. UNAM https://tecnicosacademicos.cuautitlan.unam.mx/CongresoTA/memorias2024/Mem2024_Paper07.html