SINTONIZACIÓN DE GANANCIAS E IDENTIFICACIÓN DE PARÁMETROS DE UN PÉNDULO UTILIZANDO UN MICRO ALGORITMO

Irving Luna-Ortiz¹*, M. Gabriel Villarreal-Cervantes¹ y J. Aldo Paredes-Ballesteros^1
1Centro de Innovación y Desarrollo Tecnológico en Cómputo, IPN, CDMX, México, Laboratorio de Diseño Mecatrónico Óptimo (LDMO)
* ilunao1900@alumno.ipn.mx

Resumen

Este trabajo presenta un enfoque de identificación de parámetros y sintonización de ganancias de un sistema de control en lazo cerrado de un péndulo mediante el uso de un micro algoritmo metaheurístico. Para el presente trabajo, se propone utilizar un algoritmo bionspirado, que genera micro poblaciones para resolver el problema de optimización que es la identificación de parámetros del sistema y la sintonización de las ganancias de un controlador proporcional-derivativo (PD) en una simulación numérica y después compararlo con un algoritmo canónico. De esta manera, se evaluará el rendimiento de ambos algoritmos y se probará el desempeño del micro algoritmo bioinspirado en la reducción del costo computacional y su desempeño general.

Palabras clave:Identificación de parámetros, sintonización de ganancias, micro algoritmo, poblaciones reducidas y evolución diferencial.

Introducción

En el campo del control automático, uno de los problemas más relevantes es la sintonización de las ganancias en sistemas dinámicos. Este proceso, en apariencia trivial, resulta ser complejo debido a la naturaleza no lineal de muchos de estos sistemas. La no linealidad introduce una serie de dificultades, ya que los métodos tradicionales de sintonización de controladores, como los basados en modelos matemáticos, pueden no ser aplicables o resultar ineficaces. En este contexto, la optimización surge como una estrategia viable para abordar la sintonización de estos controladores, permitiendo encontrar soluciones óptimas que garanticen un desempeño deseado. Además, la utilización de técnicas de optimización en controladores no lineales puede ser clave para enfrentar las limitaciones inherentes a los métodos convencionales, llevando así a que el sistema trabaje de la forma esperada. En el presente trabajo se propone realizar la identificación de los parámetros y la sintonización del controlador de un sistema no lineal, en el caso particular de un péndulo, mediante optimización usando micro algoritmos bioinspirados.

Optimización

Optimización es el proceso mediante el cual se obtiene el mejor resultado dentro de un problema bajo ciertas circunstancias, especificaciones o condiciones (Rao, 2019). El proceso de optimización pasa por tres etapas que son: la formulación del problema de optimización, la resolución del problema y por último su validación.

Para resolver un problema de optimización se genera una función objetivo construida a partir de sus variables de diseño y se establecen criterios como restricciones de igualdad y desigualdad, los problemas de optimización se pueden resolver con los criterios de primera y segunda derivada, usando la técnica de Karush Kuhn tucker (Rodríguez et al., 2020) o mediante algoritmos de optimización. Existen dos tipos de algoritmos de optimización, los determinísticos, que utilizan técnicas de búsqueda sistematizadas, ya sea por reglas definidas o por descenso del gradiente, como el método de Newton (Nesterov, 2013) y los estocásticos, aquellos que dependen del azar como los algoritmos bioinspirados o también conocidos como metaheurísticas que son estrategias de optimización diseñadas para resolver problemas complejos y difíciles de optimizar mediante técnicas tradicionales y estas están inspiradas en la naturaleza como en la combinación de genes (Srinivas et al., 1994), en el comportamiento de los animales (Kennedy et al., 2001) o en la evolución (Storn et al.,1997).

Sistemas de control

Según (Ogata, 1998) los sistemas de control son conjuntos de componentes que gestionan el comportamiento dinámico de un sistema mediante la regulación de la entrada, de modo que se logren resultados deseados en la salida. Existen muchos tipos de controladores, pero para el caso particular se utilizó un control proporcional derivativo (PD). Estos controladores se han utilizado a lo largo de los años, su uso data a partir de 1890, han permanecido vigentes debido a su gran efectividad en procesos ( Bennet,1993; Abbasi et al., 2017) y además por presentar simplicidad y facilidad para reajustar las variables de control (Äström et al., 1995), en (1) se presenta la ecuación de un controlador PD para el caso de regulación, donde u(t) es la señal de control, es el error en el tiempo t, K_P es la ganancia proporcional y K_D que es la ganancia derivativa.

Identificación

La identificación de parámetros de un sistema es el proceso de determinar los valores de los parámetros que caracterizan el comportamiento dinámico de un sistema a partir de datos experimentales o de observación (Rodríguez et al., 2022). Algunos objetivos de la identificación de parámetros son describir el comportamiento del sistema, obtener un modelo matemático preciso que represente el sistema físico, mejorar el control y la simulación, usando el modelo identificado para diseñar controladores efectivos y realizar simulaciones precisas, esta estimación de parámetros se pueden hacer de distintas formas: mediante el método de los mínimos cuadrados, el método de máxima verosimilitud, el filtro de Kalman, técnicas de optimización no lineal y algoritmos metaheurísticos. En este trabajo se utilizarán los algoritmos metaheurísticos o bioinspirados, para resolver el problema de identificación del robot manipulador de un grado de libertad o péndulo simple.

Sintonización

La sintonización en teoría de control se refiere al acto de seleccionar y ajustar los parámetros de un controlador, para trabajar de forma deseada. Para la sintonización de ganancias en sistemas lineales se puede realizar por métodos propuestas por Ziegler y Nichols (Ziegler y Nichols, 1942), pero en cuestión de sistemas no lineales la sintonización de ganancias se convierte en una tarea complicada. Existen cuatro clasificaciones para el ajuste de parámetros del controlador (PID) de lazo cerrado propuesto por Moradi y Johnson (Johnson et al, 2005), pero en el presente trabajo utilizaremos otra clasificación propuesta en (Villarreal et al., 2016) y en (Rodríguez et al., 2020), que permite conocer qué técnica de sintonización se va a utilizar dependiendo del problema, la clasificación la basa en los cuatro métodos siguientes:

• 1. Métodos analíticos.
• 2. Métodos heurísticos.
• 3. Métodos de optimización.
• 4. Métodos adaptables.

Para el presente trabajo se utilizará el Método No. 3, donde se establece a la identificación de parámetros y la sintonización como un problema de optimización que se resuelve mediante un optimizador para encontrar un conjunto adecuado de parámetros del controlador (Flores et al., 2020).

Objetivo

Realizar la sintonización de ganancias de un controlador proporcional-derivativo para el caso de regulación para un péndulo simple e identificar los parámetros de dicho sistema dinámico en simulación numérica, todo esto mediante el uso de micro algoritmos bioinspirados.

Además, se llevará a cabo una comparación detallada entre los resultados obtenidos con los micro algoritmos y los algoritmos canónicos, evaluando el desempeño.

Materiales y métodos

A continuación, se presentan los materiales y métodos utilizados para poder realizar y fundamentar los experimentos que permitan alcanzar el objetivo del presente trabajo.

Microevolución Diferencial (µ-DE)

El algoritmo de evolución diferencial para micro poblaciones fue tomado de (Viveros et al., 2012). La diferencia que existe entre evolución diferencial canónico y para micro poblaciones, además del tamaño de la población, es que cuenta con un ciclo iterativo interno, el cual tiene como condición de entrada a este bucle cumplir con cierto número de generaciones al cual se le llama generaciones de reemplazo. Una vez entrado a este bucle se sustituyen los individuos que tengan las peores evaluaciones de la función objetivo por nuevos individuos, generados aleatoriamente, lo que permite traer diversidad a la población y así evitar una convergencia prematura a un óptimo local (Tabla 1).

Una vez descrito el pseudocódigo anterior, se presenta el pseudocódigo de µ-DEreb1b, que es la combinación del mecanismo de reemplazo con DE canónico (Tabla 2).

Modelo dinámico del robot manipulador de 1 grado de libertad

En esta sección se procede a obtener el modelo dinámico de un péndulo simple o visto de otra forma como un robot R de un grado de libertad. En la Figura 1 se observa un esquema representativo del robot manipulador de un grado de libertad donde se usa el ángulo de oscilación como coordenada generalizada y también se pueden apreciar los parámetros dinámicos del sistema, donde m es la masa del eslabón, L_cm es la longitud del centro de masa, 𝐼𝑧 es la inercia del eslabón y 𝜃 es la posición angular.

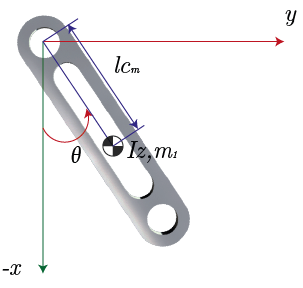
Figura 1. Modelo representativo del robot manipulador de un grado de libertad.

A continuación, se procede a utilizar las ecuaciones de Euler-Lagrange descritas en (2) para obtener la dinámica del sistema, en donde 𝜏∈𝑅^𝑛 es el vector de pares.

En (3) se procede a calcular el lagrangiano del robot manipulador de un grado de libertad:

En donde 𝐿 es el lagrangiano, T es la energía cinética y 𝑉 es la energía potencial, y se procede calcularlo obteniendo la energía cinética en la ecuación (4).

Donde 𝑣 es la velocidad lineal definida en (5).

Sustituyendo (5) en (4) obtenemos (6) que es la energía cinética del sistema.

En (7) se procede a calcular la energía potencial.

Donde ℎ es la altura del sistema y g es la aceleración debido a la gravedad. En (8) se establece la energía potencial.

Por lo que el lagrangiano resulta en (9).

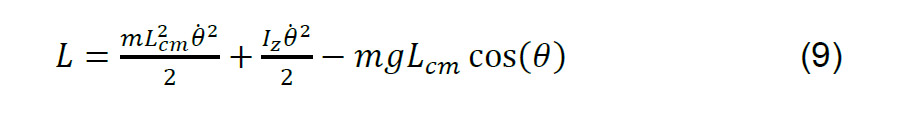
Se resuelve primero haciendo la parcial del lagrangiano con respecto de 𝜃̇:

Enseguida se calcula la derivada con respecto del tiempo de la parcial con respecto a la velocidad angular del lagrangiano:

A continuación, se obtiene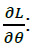

Sustituyendo a (13) y (12) en (2) se obtiene (14)

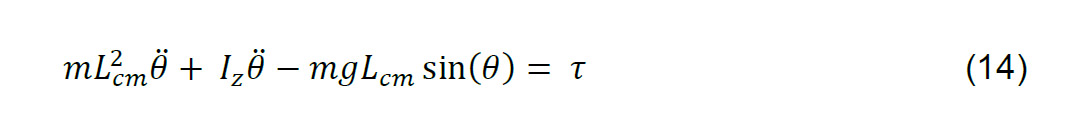
Considerando la dinámica en lazo cerrado en (15)

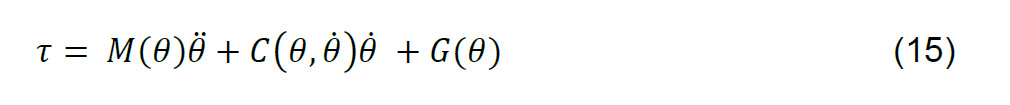
Experimentos

En esta sección se plantean las bases y las condiciones iniciales de los experimentos, tanto para identificación de parámetros como para la sintonización de ganancias del controlador, debido a que utilizaremos los algoritmos bíoinspirados de evolución diferencial, por sus siglas en inglés DE y evolución diferencial para micro poblaciones µ-DE, se propondrán estos dos problemas como problemas de optimización matemática.

Identificación

Para resolver el problema de identificación de parámetros, se comparan las salidas del sistema real y el sistema simulado numéricamente, utilizando una estimación aproximada de los parámetros físicos para el sistema simulado. Al aplicar una señal de control acotada y observando la salida de ambas, se evalúa si el comportamiento del sistema simulado se asemeja al real, calculando el error como la diferencia entre ambos sistemas, la salida del sistema real menos la salida del sistema simulado. Luego, se emplea la métrica Integral del Error al Cuadrado (ISE, por sus siglas en inglés) como función objetivo a minimizar. Un micro algoritmo de optimización genera los valores que se asignan a los parámetros, asignados en el vector p_id=[m,L_cm,I_z ]^T como las variables de diseño en el problema de optimización presentado en (17), donde x ̇=f(x)-g(x)u es la dinámica representada en el espacio de estados.

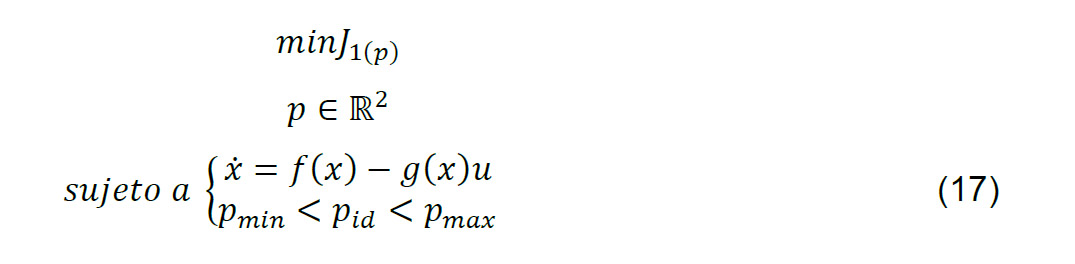
Sintonización

Para el problema de sintonización se aborda mediante (18), donde el vector 𝑝=[𝐾𝑝,𝐾𝑑]^𝑡 son las ganancias del controlador.

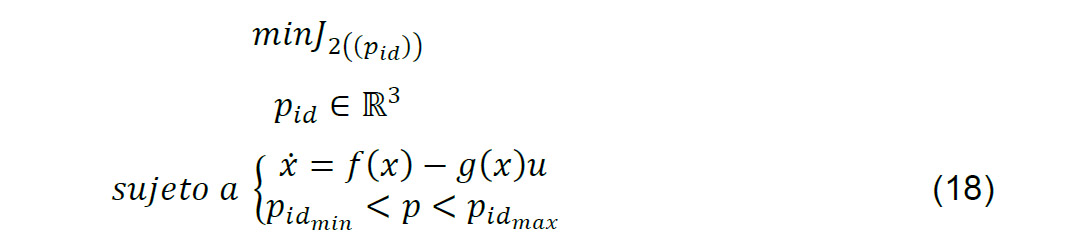
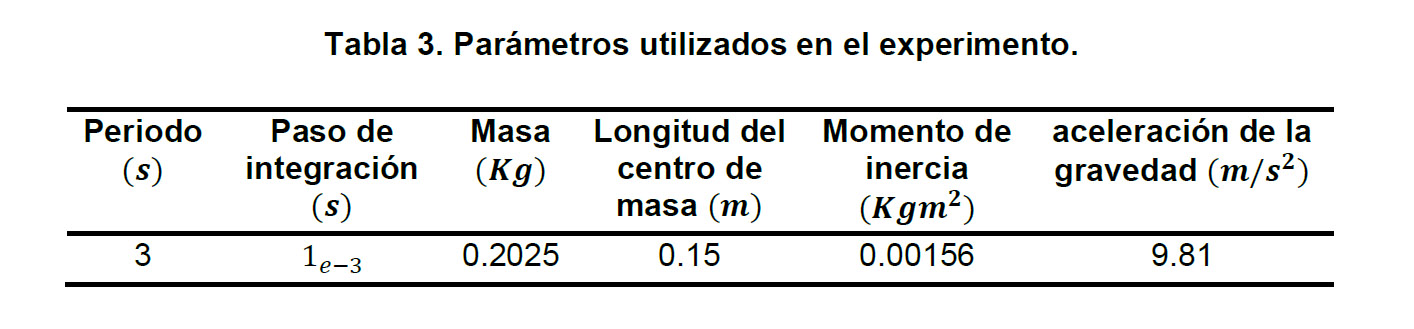
Cabe mencionar que los parámetros (Tabla 3) masa del eslabón, la longitud del centro de masa del eslabón y el momento de inercia mostrados en la tabla anterior, son obtenidos de un sistema físico que se encuentra en el laboratorio de diseño mecatrónico óptimo en el CIDETEC del Instituto Politécnico Nacional.

A continuación, se aprecia en la siguiente Tabla 4 los parámetros utilizados para el problema de identificación en los algoritmos de optimización, evolución diferencial y evolución diferencial para micro poblaciones:

Ahora en la Tabla 5 se observan los parámetros utilizados para el problema de sintonización de un controlador PD con los algoritmos de optimización de Evolución Diferencial y Evolución Diferencial para micro poblaciones:

La señal de entrada conmutada 𝑈(𝑡), utilizada para el problema de identificación de parámetros, se muestra en la Figura 2.

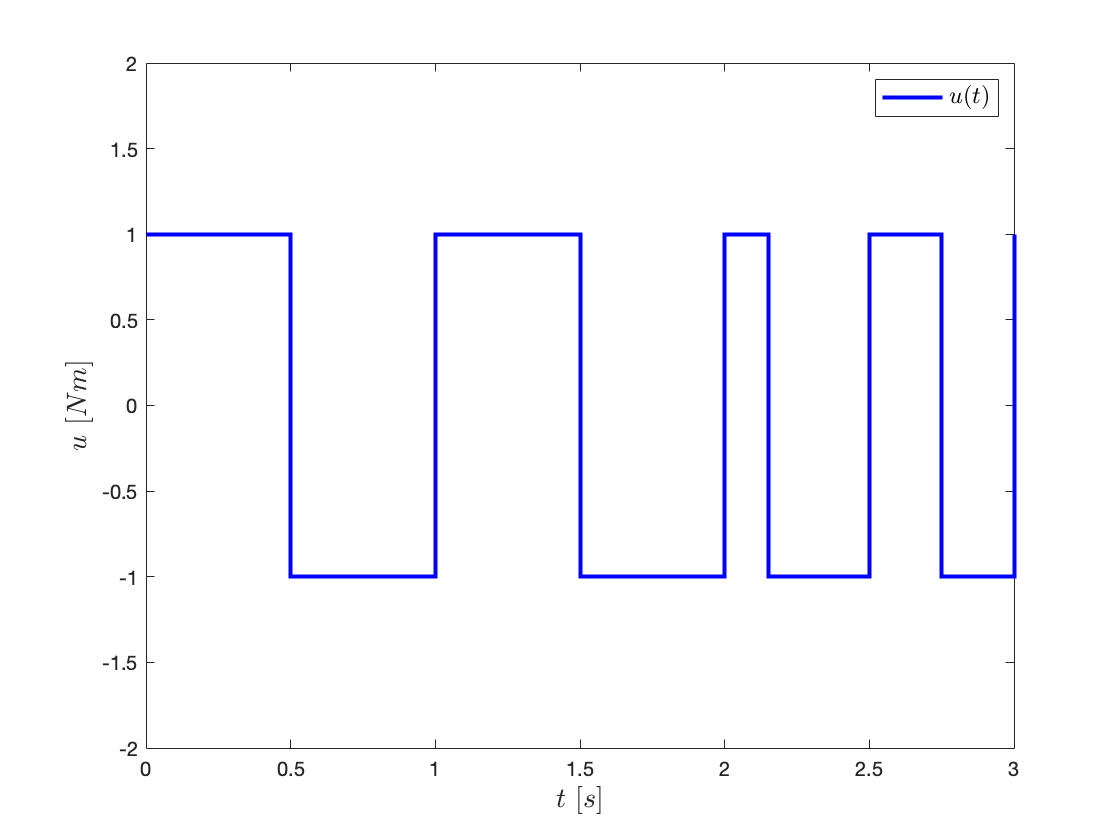
Figura 2. Señal de entrada conmutada 𝑼(𝒕).

Estos experimentos fueron realizados en el entorno de programación de MATLAB, los algoritmos y funciones fueron desarrolladas completamente, sin utilizar funciones preestablecidas por algún paquete o librería, se ejecutaron sobre un procesador Intel(R) Core (TM) i5-4200U CPU @ 1.60GHz, con 16 Gb de RAM, procesador de 64 bits x64 y sistema operativo Windows 10 Home.

Resultados

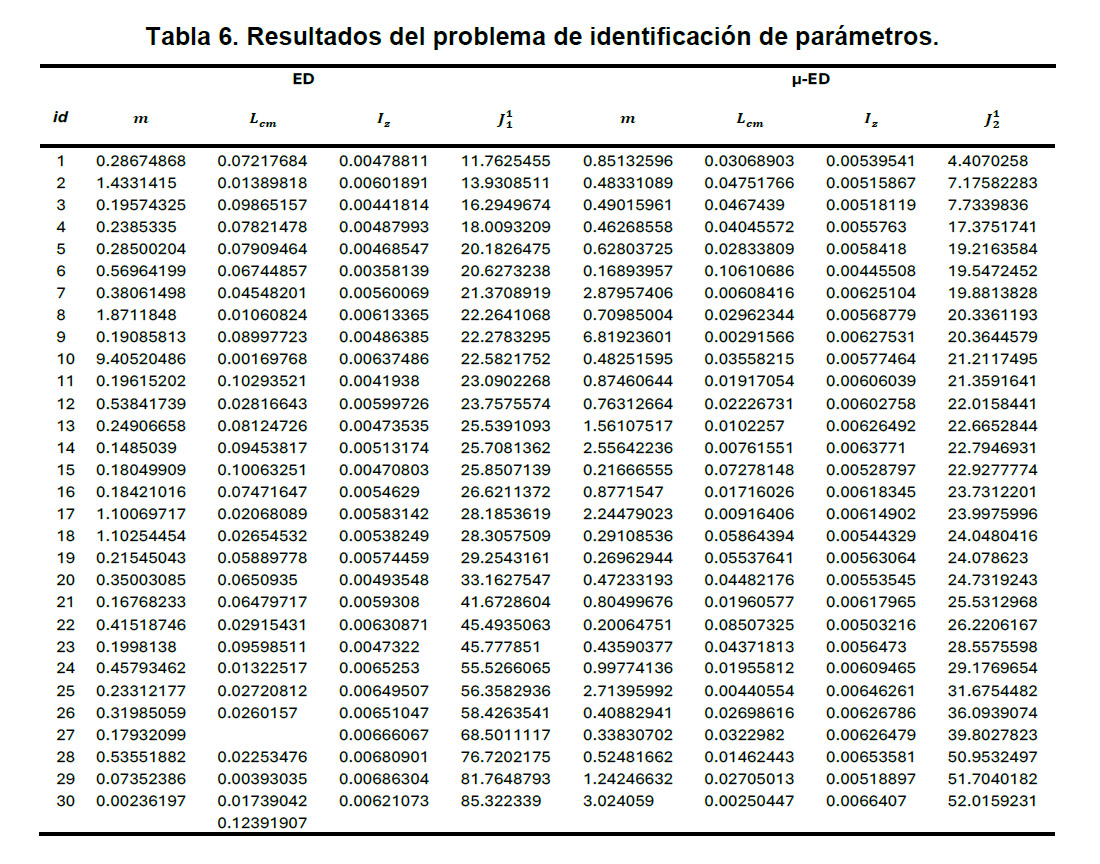
En esta sección se muestran los resultados obtenidos de los problemas de identificación de parámetros y el de sintonización de ganancias del controlador con los algoritmos, DE y 𝜇-DE. En la Tabla 6, se muestran los resultados del problema de identificación de parámetros, se presentan los valores obtenidos a través de 30 corridas independientes las cuales son suficientes debido a que el modelo solo incluye parámetros básicos para la identificación y en la sintonización se puede observar convergencia al punto de referencia. Se muestran las variables de diseño y la evaluación de la función objetivo para los algoritmos implementados (DE y µ-DE). Cada sección incluye cuatro columnas: masa” m”, longitud al centro de masa” L_cm”, momento de inercia” 𝐼_𝑧” y una columna” id” que indica los valores por cada corrida, como se muestra a continuación:

Tabla 6. Resultados del problema de identificación de parámetros.

En la Tabla 7 se aprecian los resultados estadísticos para el valor promedio de la Figura 6.

En la Figura 3 se describe la posición del sistema con los parámetros del péndulo reales y el mejor resultado obtenido por los algoritmos DE y µ-DE, cuando se le inyecta la señal de entrada U(t), como se muestran a continuación:

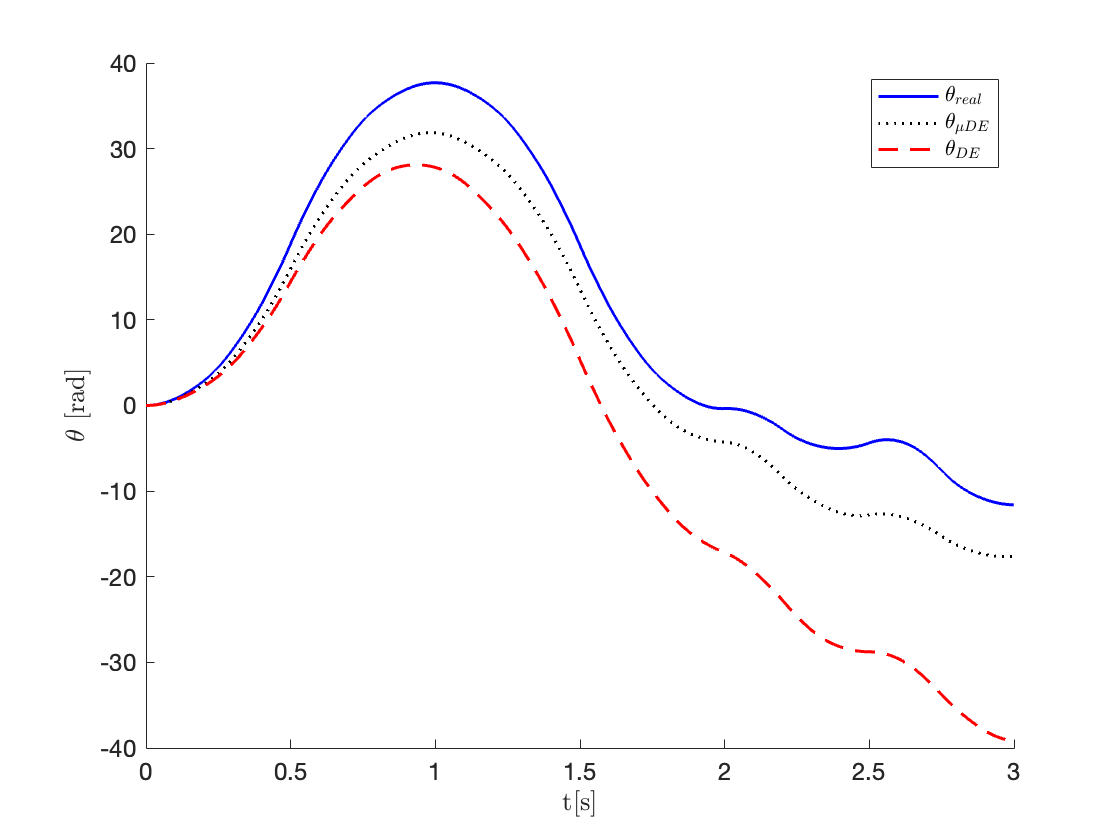
Figura 3. Identificación valor promedio.

Para el experimento de sintonización de ganancias de un controlador PD se presenta la Tabla 8, con dos secciones una con los resultados obtenidos por DE y la otra sección para µ-DE, cada sección cuenta de tres columnas en donde se registran los valores obtenidos por los algoritmos que son, la ganancia proporcional K_p, la ganancia derivativa K_d, el valor de la evaluación de la función objetivo para la sintonización J₂ y una columna llamada id, que nos dice el valor mínimo obtenido por cada corrida.

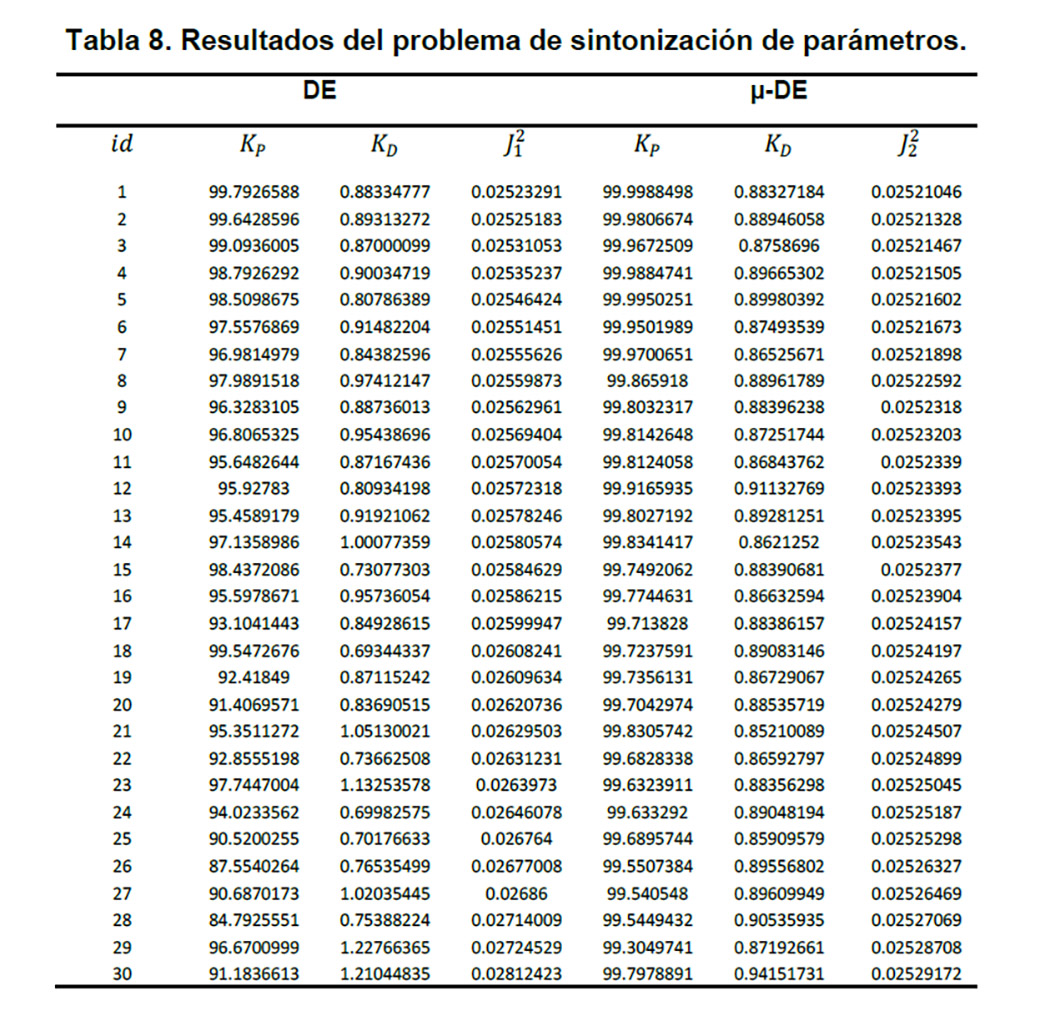
Los resultados estadísticos se presentan en la Tabla 9.

A continuación, en la Figura 4, se muestran las curvas que describen la variación de la posición con respecto al tiempo, la línea punteada describe la sintonización de ganancias realizada por DE y la línea continua describe la realizada por µ-DE, en donde se observa como las curvas llegan a la referencia que es 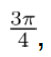pero µ-DE llega con menos sobre impulso y un poco más rápido que DE.

Figura 4. Sintonización valor promedio.

Discusión

En esta sección, se realizará un análisis de resultados con la finalidad de observar las diferencias encontradas al resolver el problema de identificación de parámetros del sistema físico robot manipulador de un grado de libertad y el problema de sintonización de ganancias de un control PD, para un problema de control de regulación.

Como se puede observar en la Tabla 6, en las treinta corridas el valor de la evaluación de la función objetivo obtenido fue menor para µ−DE contra el valor obtenido por , además que en la Tabla 7, donde se muestran los valores promedio, también 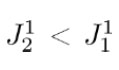y por último se puede observar en la Figura 4, que la curva generada por los parámetros obtenidos por el algoritmo de evolución diferencial para micro poblaciones, es la que se aproxima más a la curva con los parámetros reales del sistema, por lo que se puede decir que para el problema de identificación de parámetros aquellos obtenidos con µ − DE presentan un mejor desempeño que los obtenidos con DE.

Para el problema de sintonización de ganancias de un control PD para un problema de control de regulación, el cual pretende llevar al robot manipulador de un grado de libertad (péndulo simple) a la posición de 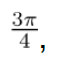, en las Tablas 6 y 7, se observa que en las treinta corridas, los valores de la evaluación de la función objetivo obtenidas por µ − DE, presentaron mejor desempeño que las obtenidas por DE, también se observa en la tabla 8, que 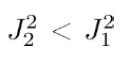y por último, como se puede observar en las Figuras 5 y 6, la curva que describe el problema de regulación con las ganancias obtenidas por µ − DE llega más rápido al estado estacionario, por lo que podemos concluir que las ganancias obtenidas por evolución diferencial presentan un buen desempeño en el control de regulación, pero las que se obtuvieron con µ − DE presentan un mejor desempeño.

Conclusión

En el presente trabajo se realizó una identificación de parámetros de un péndulo simple y además se realizó una sintonización de ganancias todo esto por medio de la optimización usando el micro algoritmo de evolución diferencial y después se realizó una comparativa entre µ − DE y DE debido a que el algoritmo seleccionado presenta un buen desempeño al realizar las tareas de identificación de parámetros y la de sintonización de ganancias de un controlador PD con respecto al algoritmo canónico, podemos inferir que esta técnica presentara un buen desempeño en un sistema real.

Agradecimientos

Se extiende un cálido agradecimiento al Congreso Nacional de Tecnología CONATEC 2024, por el espacio para la divulgación científica.

Referencias

• Abbasi, E., Naghavi, N. (2017). Offline auto-tuning of a PID controller using extended classifier system (XCS) algorithm.
• Åström, K.J., Hagglund, T. (1995). PID controllers: Theory, design, and tuning.
• Bennett, S. (1993). A history of control engineering, 1930-1955. No. 47). IET.
• Flores, C.G., Rodríguez, M.A., Aldape, P.M., Villarreal, C.M.G. (2020). Optimized path-planning in continuous spaces for unmanned aerial vehicles using meta-heuristics. IEEE Access, 8: 176774-176788.
• Johnson, M.A., Moradi, M.H. (2005). PID control. Springer.
• Kennedy, J., Eberhart, R.C., Shi, Y. (2001). Chapter seven - The particle swarm. In J. Kennedy, R.C. Eberhart, Shi Y. (Eds.), Swarm intelligence (pp. 287–325). Morgan Kaufmann.
• Nesterov, Y. (2013). Gradient methods for minimizing composite functions. Mathematical Programming, 140(1): 125-161.
• Ogata, K. (1998). Ingeniería de control moderna. Vol. 3. Prentice-Hall.
• Rao, S.S. (2019). Engineering optimization: Theory and practice. John Wiley & Sons.
• Rodríguez, M.A., Mezura, M.E., Villarreal, C.M.G., Aldape, P.M. (2020). Multi-objective meta-heuristic optimization in intelligent control: A survey on the controller tuning problem. Applied Soft Computing, 93: 106342.
• Rodríguez, M.A., Villarreal, C.M.G., Serrano, P.O., Solís, R.J., Silva, O.R. (2022). Optimal tuning of the speed control for brushless DC motor based on chaotic online differential evolution. Mathematics, 10(12).
• Srinivas, M., Patnaik, L. M. (1994). Genetic algorithms: A survey. Computer, 27(6): 17-26.
• Storn, R., Price, K.V. (1997). Differential evolution – A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11: 341-359.
• Villarreal, C.M.G., Alvarez, G.J. (2016). Off-line PID control tuning for a planar parallel robot using DE variants. Expert Systems with Applications, 64: 444-454.
• Viveros, J.F., Mezura, M.E., Gelbukh, A. (2012). Empirical analysis of a micro-evolutionary algorithm for numerical optimization. International Journal of Physical Sciences, 7(8): 1235-1258.
• Ziegler, J.G., Nichols, N. B. (1942). Optimum settings for automatic controllers. Trans. ASME, 64(11).

Séptimo Congreso Nacional de Tecnología 16, 17 y 18 de octubre de 2024,
celebrado en formato virtual

---

Excepto donde se indique lo contrario esta obra está bajo una licencia Creative Commons Atribución No comercial, No derivada, 4.0 Internacional (CC BY NC ND 4.0 INTERNACIONAL).
https://creativecommons.org/licenses/by-nc-nd/4.0/deed.es

FORMA SUGERIDA DE CITAR:

Luna-Ortiz, I., Villarreal-Cervantes, M. G., y Paredes-Ballesteros, J. A. (2024). SINTONIZACIÓN DE GANANCIAS E IDENTIFICACIÓN DE PARÁMETROS DE UN PÉNDULO UTILIZANDO UN MICRO ALGORITMO. MEMORIAS DEL CONGRESO NACIONAL DE TECNOLOGÍA (CONATEC), Año 7, No. 7, septiembre 2024 - agosto 2025. Facultad de Estudios Superiores Cuautitlán. UNAM https://tecnicosacademicos.cuautitlan.unam.mx/CongresoTA/memorias2024/Mem2024_Paper09.html