PERTURBACIÓN EN LA DISTRIBUCIÓN RECTANGULAR EN LA
ESTIMACIÓN DE LA INCERTIDUMBRE DE MEDIDA

Gabino Estevez-Delgado^1*, Joaquin Estevez-Delgado² y José Eduardo Cuevas-Cuevas^1
1Universidad Michoacana de San Nicolás de Hidalgo. Facultad de Químico Farmacobiología. ²Universidad Michoacana de San Nicolás de Hidalgo. Facultad de Ciencias Físico Matemáticas
*gabino.estevez@umich.mx

Resumen

Una de las variables de influencia en la estimación de la incertidumbre de medida en los procesos de calibración de instrumentos de medición analógicos, es la distribución asociada a la resolución cuya distribución de probabilidad es rectangular. Sin embargo, los valores de alcance de medición de los instrumentos o materiales pueden tener variaciones en su ámbito de trabajo en los extremos debido al deterioro del propio instrumento o de los materiales de referencia, lo que impacta las mediciones, principalmente cuando se hace uso de equipos que si no se realiza una buena validación de la deriva instrumental pueden comprometer los resultados. En esta investigación, se realiza un análisis de la perturbación de la distribución de probabilidad rectangular. Se hace lo anterior, antes de introducirla a la ecuación de propagación de error, esto lo recomienda la guía internacional para la estimación de la incertidumbre medida, lo cual permite realizar una mejor consideración de la incertidumbre, sin ignorar el deterioro que impacta a la deriva instrumental y en consecuencia a las mediciones. A fin de realizar un análisis puntual del efecto de la perturbación en una medición de un cálculo de la densidad de un medio contenido en un cilindro, utilizando un vernier para el diámetro, una regla para la altura y un termómetro, todos instrumentos digitales, se analiza la perturbación del termómetro para el termopar que adquiere los datos de medida del medio. Se encontró que la incertidumbre aumenta al tomar el presupuesto considerando con los grados efectivos de libertad dados por la ecuación de  Welch-Satterthwaite, siendo esta una ecuación útil para complementar las contribuciones de todas las fuentes de incertidumbre incluyendo la de tipo rectangular.

Palabras clave:Palabras clave: Ley de propagación de errores, deriva instrumental, coeficiente de sensibilidad.

Introducción

Las exigencias para las empresas que se encuentran acreditadas son cada vez mayores, principalmente en materia de metrología legal y científica. Lo que demanda que las empresas tengan que realizar esfuerzos importantes para mantener su sistema de gestión de calidad trazable, no sólo en los resultados de las mediciones sino en los sistemas de comparación internacional entre empresas. Si bien, estas exigencias pueden parecer demandantes, son la actualización en infraestructura y trazabilidad al sistema internacional de unidades lo que ofrece un mercado atractivo, dado que los usuarios demandan variabilidad mínima en lo que obtienen y que, a su vez, se traduce en tener resultados confiables que serán heredados a próximos usuarios de los servicios o vienes que obtienen. Así, por ejemplo, el mantenimiento de equipos, la sustitución, el remplazo y la evaluación del sistema de calidad se ha traducido en metodologías como lo son las guías técnicas de validación de los métodos, calificación metrológica (CM) y la calificación de equipos e instrumentos de medición analítica (CEIMA), entre otras. Ante la diversidad de exigencias, se han generado guías técnicas apropiadas, en el mejor de los casos, para instrumentos y métodos específicos (Velychko y Gordiyenko, 2019).

Por otro lado, pero complementando las exigencias dadas por la metrología científica, alrededor de las mediciones realizadas en sistema de gestión de calidad regulados por estándares internacionales, tal como ISO 17025, se encuentra el teorema de límite central (Bianchi y Secco, 2021). Este establece que para un conjunto de n mediciones independientes 𝑥₁,𝑥₂,𝑥₃,…,𝑥_n sólo es necesario presentar los valores esperados y variación poblacionales (𝜇,𝜎²), respectivamente, lo que comúnmente dentro del campo de la metrología son análogos al error de medida y la incertidumbre expandida (Damasceno y Couto, 2018). Siendo uno de los fundamentos principales en las mediciones realizadas dentro del sistema metrológico científico y legal (Masharipov et al., 2024).

Derivado de la aplicación del teorema de límite central, utilizado ampliamente dentro de la estadística paramétrica, se expande su aplicación dentro de la metrología científica, asignando diversas funciones de densidad de probabilidad, seccionándose en dos tipos: la que depende de las mediciones directas tomadas de los datos experimentales y llamadas incertidumbres tipo A, principalmente la repetibilidad y reproducibilidad, y las que se asocian de las características metrológicas del instrumentos como son la resolución, la deriva instrumental, histéresis y la información reportada en los certificados de calibración, entre los más importantes. De manera general, toda la información aportada por las incertidumbres tipo A y B son asociadas como componentes que serán tratadas como variabilidades de carácter geométrico a través de la ley de propagación de errores a fin de obtener una componente representativa de todas las variables de influencia que afectan a la dispersión de los datos de medida (Kirkup y Frenkel, 2006).

El tratamiento de las distribuciones de probabilidad asociadas a las mediciones, particularmente aquellas usadas producto de las características instrumentales, son de interés particular debido a que ello depende la calidad de las mediciones realizadas, lo que representa la diferencia entre las mediciones realizadas entre un laboratorio y otro y no sólo a la resolución de los instrumentos de medición y el tamaño de muestra (Demeyer et al., 2022). Esa parte de la diferencia competitiva en la estimación de la incertidumbre es aportada principalmente por la buena estimación de los grados de libertad, que actualmente dentro del campo metrológico lo presenta la fórmula W-S de Welch-Satterthwaite (Cox y O’Hagan, 2022).

Sin embargo, aun cuando la fórmula W-S de Welch-Satterthwaite es una expresión que aporta valor en la determinación del valor de confianza, asociado como factor de cobertura, se requiere tomar algunas consideraciones, como son los datos de las mediciones directas de los instrumentos. En la incertidumbre expandida presentada, después de aplicar la ley de propagación de errores, es necesario tomar las mediciones directamente de los instrumentos de medición. Por ejemplo, instrumentos de carácter digital se les asocia la distribución rectangular, que, considerando el teorema de límite central, se apreciara un valor constante para la variabilidad asignándole una variación que va como:

Donde 𝑢 es la incertidumbre estándar para una distribución rectangular, en tanto que Δ𝑎 es la resolución de la escala de medición del instrumento o la determinación asociada a los estudios de reproducibilidad contra repetibilidad. Lo que puede ser modificado por las condiciones de trabajo, en el caso de sensores usados en la medición directa del instrumento y que no siempre se ven considerados como parte del deterioro natural, llamada deriva instrumental. Es conocido que, la gran mayoría de las personas consideran que un instrumento puede seguir midiendo si este aún emite resultados en la pantalla, pero realmente este no siempre es un valor real a menos que se realice una validación de los resultados emitidos en la pantalla.

Como parte de la búsqueda de respuestas de lo que ocurre con el deterioro de un sensor de temperatura de un termómetro utilizado, se puede valorar los valores históricos del termómetro a lo largo del tiempo e incorporarlos como una perturbación a las mediciones realizadas.

Objetivo

Realizar un estudio comparativo entre dos mediciones volumétricas midiendo como parte de la variable de influencia la temperatura del medio para un cilindro que contiene agua, con la afectación del deterioro del termómetro debido a su termopar y sólo considerando la distribución rectangular asociada a la pantalla del instrumento.

Materiales y métodos

Se realizan 10 mediciones que permiten valorar la densidad del líquido contenido, para el caso del volumen se utilizó: una regla para medir la altura del cilindro y un vernier para la estimación del diámetro. En tanto que, para la medición de la masa se realizaron 10 mediciones con una balanza analítica. A fin de monitorear alguna posible influencia de la temperatura, se monitorearon las posibles variaciones con un termómetro digital. Los datos instrumentales se presentan en la Tabla 1.

Tabla 1. Propiedades de resolución e incertidumbre de los instrumentos.

Característica	Datos de la regla	Datos del vernier	Datos de la balanza	Datos Del termómetro
Resolución	0.1 mm	0.5 mm	0.0001g	0.1 °C
Incertidumbre certificada	0.029 mm	0.037 μm	0.000001 g	0.05 °C

---

Nota. La incertidumbre certificada es proporcionada de los certificados de calibración para cada instrumento.

Las mediciones realizadas se presentan en la Tabla 2.

Tabla 2. Repetibilidad de las mediciones realizadas para el cilindro y sus condiciones de condiciones ambientales de temperatura y humedad.

Medición	Repetibilidad de la regla (mm)	Repetibilidad del Diámetro con el Vernier (mm)	Repetibilidad de la balanza analítica (g)	Temperatura (°C)	Humedad (%HR)
1	100.1	50.5	0.0019	19	55
2	100.2	50.0	0.0018	20	56
3	100.1	50.5	0.0019	19	57
4	100.0	50.0	0.0019	20	58
5	100.1	50.0	0.0018	20	59
6	99.9	49.5	0.0019	21	60
7	100.1	50.5	0.0019	20	61
8	99.9	50.5	0.0019	20	62
9	100.0	49.5	0.0019	20	63
10	99.8	50.0	0.0019	20	64
Promedio	100.0	50.1	0.00188	19.9	59.5
Desviación estándar	0.12	0.4	4.21637E-05	0.6	3.0

Considerando que la balanza analítica y el vernier son instrumentos cuya resolución son digitales, a estos se les asociará una distribución de probabilidad rectangular, al igual que para el termómetro, siendo este último un periférico que en principio no se considera directamente en el modelo físico para la ecuación de la densidad. Por otro lado, la regla a considerar es asociada a una función de densidad triangular por ser un instrumento de carácter analógico.

Abonando a la estimación del cálculo del presupuesto de la incertidumbre, se determina primeramente el modelo físico de las mediciones, en este caso, la densidad es considerada como:

Siendo m la masa promedio obtenida de las mediciones realizadas en la balanza analítica, en tanto que el volumen (V) a su vez se obtiene de considerar que al tratarse de un contenido cilíndrico como:

De tal forma que, al considerar la ecuación (3) en (2), tendremos:

Como se observa en esta última ecuación, no existe la influencia de la temperatura, lo cual, de haber un buen control de las condiciones ambientales no debería de ser modificada la densidad. De esta manera, hagamos un análisis de la incertidumbre, en un primer momento sin considerar la posible afectación de los registros de la temperatura y humedad.

Considerando la ley de propagación de errores, de la forma más general, para el caso de la incertidumbre combinada, se tiene:

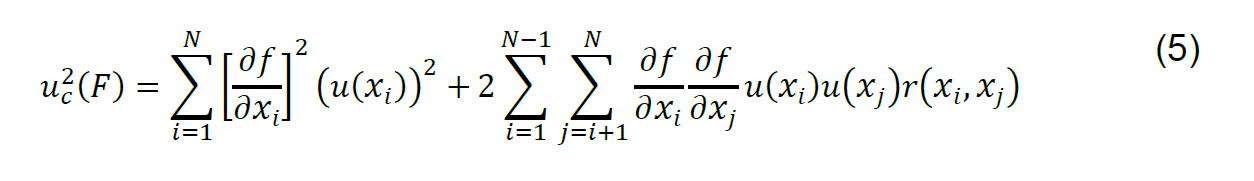
Donde 𝑢(𝑥_𝑖) son las incertidumbres asociadas a las características del instrumento y de la medición y 𝑟(𝑥_𝑖,𝑥_𝑗) el coeficiente correlación de Pearson, de ser significativa la correlación entre las variables.

Una simplificación, en abreviaturas, es dada cuando se considera que 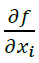representan el cambio de la variable de medida con respeto a su variación por lo que a este se le designa con el nombre de coeficiente de sensibilidad, es decir, , de esta forma la ley de propagación de errores (5) se expresa como:

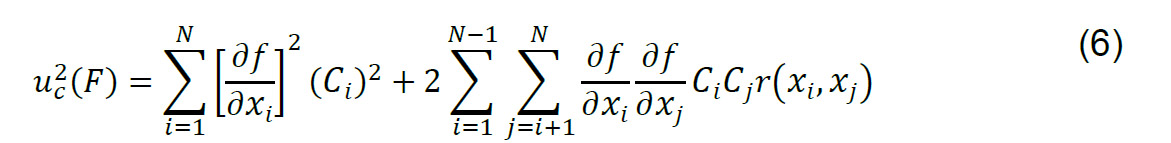
Cuando no existe correlación entre las variables de influencia, la expresión se reduce a:

Siendo esta una ecuación bastante sencilla de operar.

Sin embargo, se requiere calcular los coeficientes de sensibilidad del modelo físico. Para nuestro caso tendríamos:

Por otro lado, el factor de cobertura correspondiente, que nos habla del nivel de confianza dentro de una distribución normal se obtiene de la ecuación siguiente, conocida como la incertidumbre combinada, que es la que nos es dada en los procesos de calibración en los certificados o informes de calibración:

Es precisamente el valor de k, lo que determina la competencia de los laboratorios de calibración. Al realizar cálculos adicionales, con la fórmula de Welch- Satterthwaite, el nivel de confianza de las mediciones ampara al menos el 95% de confianza (k=2), utilizada en la ecuación (11). Para realizar mejores estimaciones estadísticas se consideran los grados efectivos de libertad asociados a las funciones de densidad de probabilidad y se hace uso de la fórmula de Welch-Satterthwaite, para tener una estimación lo más cercana posible a las condiciones de laboratorio, dada como:

Donde 𝜈_𝑖 corresponde a los grados efectivos de libertad para cada tipo de contribución de las fuentes representativas, y 𝜈_𝑒𝑓 representa los grados efectivos. Por último, se hace uso de la distribución t-student, de tal forma que la incertidumbre expandida toma la forma:

Retomando los datos de las Tablas 1 y 2 y las consideraciones para los coeficientes de sensibilidad se tiene lo siguiente (Tabla 3).

Tabla 3. Estimación de la incertidumbre considerada en la ley de propagación de errores para la obtención de la densidad volumétrica.

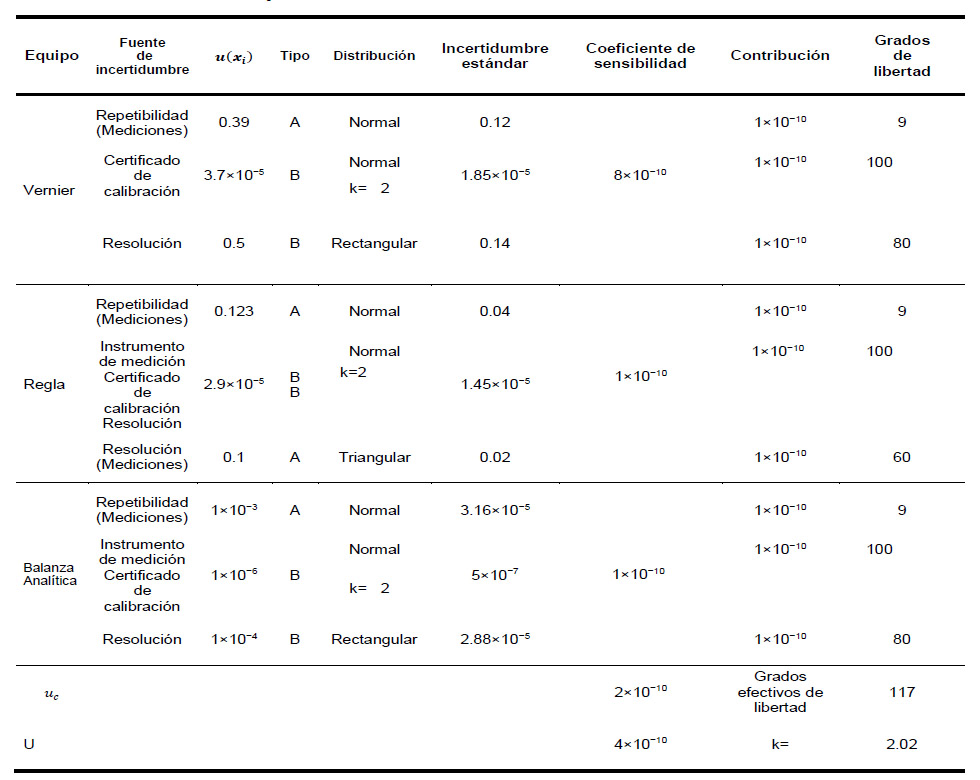
Nota. La obtención de la K es un factor de cobertura que representa más del 95% de confianza.

Resultados

Hasta el momento, se ha obtenido estimación del presupuesto de la incertidumbre, sin considerar alguna posible correlación. Sin embargo, al calcular el coeficiente de correlación de Pearson de los datos obtenidos de la temperatura y las mediciones con el Vernier, que aun cuando el valor es de 0.69 este quizá pueda indicar una tendencia y procederemos a incorporarlo en el análisis de la variabilidad para el caso de la distribución asociada, de tipo rectangular.

Recordemos que la función de densidad de probabilidad asociada para la distribución rectangular es dada como el de la figura 1, correspondiente a un esquema gráfico.

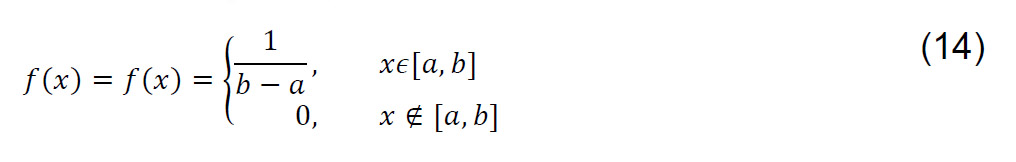
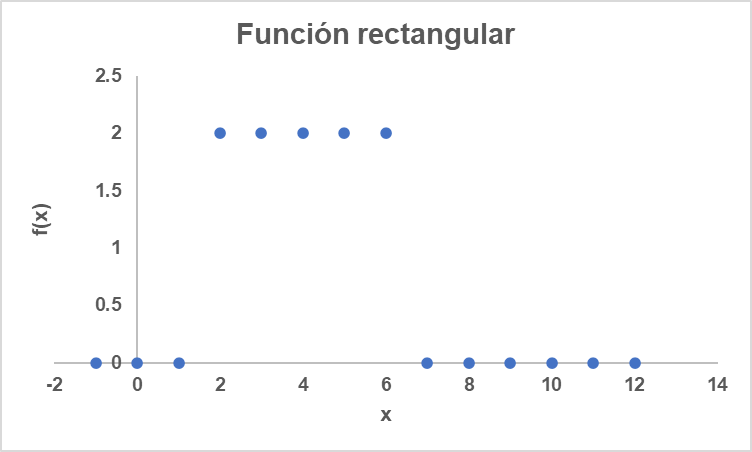
Figura 1. Función rectangular o uniforme.

Se puede afectar ligeramente la consideración de esta uniformidad para la resolución si se aplica la perturbación lineal en el intervalo de las mediciones realizadas del rango de temperaturas de 19 °C a 21 °C, cuyo error de medición, según el certificado de origen para el termómetro, es de 0.01 °C. De esta forma el valor a corregir correspondería al valor de la convolución de la función:

En tanto que, la función original rectangular para la resolución es dada como:

En el ámbito de trabajo entre 0 °C a 45 °C.

Al aplicar la convolución para la corrección de los errores instrumentales, se tiene:

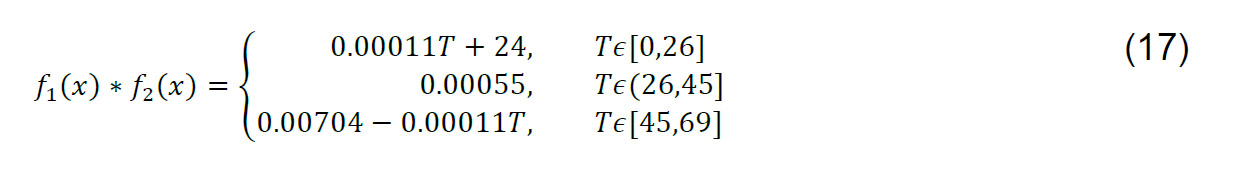
Si bien, existen intervalos de corrección, solo se aplicará la corrección con la función en el intervalo de [0,26] que corresponde al intervalo de las mediciones estimadas entre 19 °C a 24 °C, obteniéndose las incertidumbres como (Tabla 4):

Tabla 4. Estimación de la incertidumbre considerada en la ley de propagación de errores para la obtención de la densidad volumétrica, considerando la variación que puede dar el termómetro.

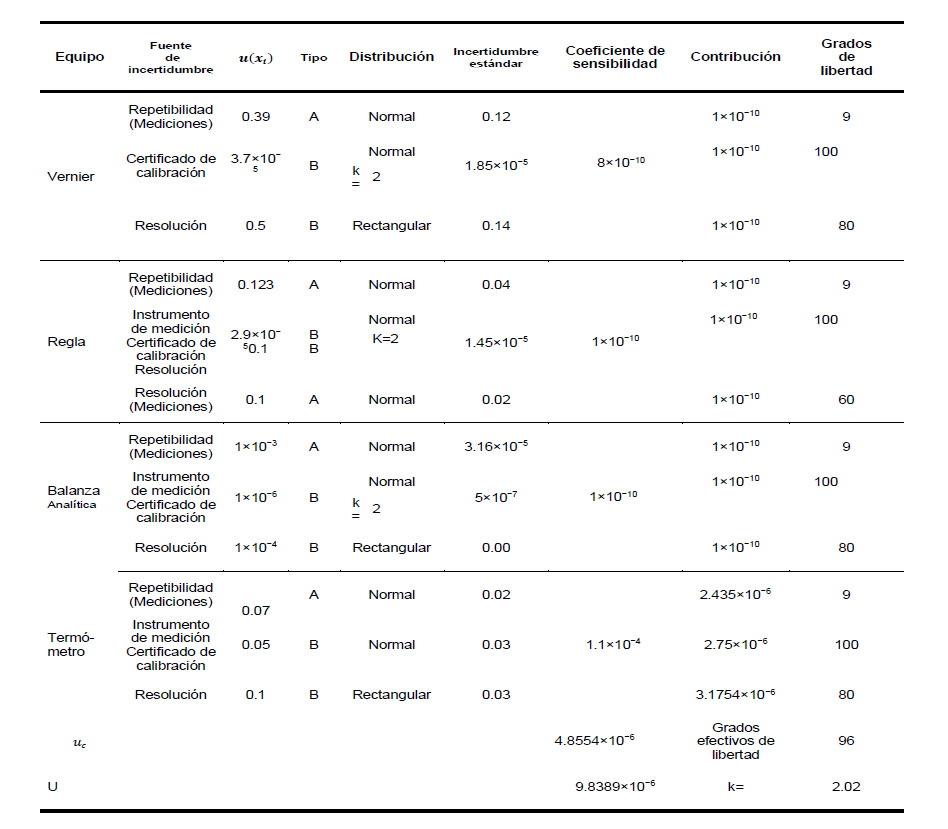
Nota. A diferencia de la Tabla 3, esta incluye la aportación de la temperatura en la medición.

Discusión

Se observa que las contribuciones, si bien, al comparar las mediciones de temperatura, no modificaron significativamente la incertidumbre, sí se vio reflejada una modificación en los grados efectivos de libertad, siendo menores cuando se consideran una perturbación como la aplicado mediante la ecuación (17), lo anterior, producto de las contribuciones debidas probablemente a la deriva instrumental del termómetro. Es de destacar que las contribuciones por interpolación son comúnmente despreciadas por los laboratorios de ensayo y calibración debido a que las guías técnicas suelen presentar los casos más simples y no siempre los más reales, ecuación (7) en lugar de (6), lo que pueden generar sobre estimación de la incertidumbre de medida. Con los resultados obtenidos se observa que los grados efectivos de libertad considerados en la fórmula de Welch-Satterthwaite si se modifican, por lo que, de manera ética, conviene no despreciar las correlaciones, sino por el contrario, incluirlas a fin de tener una mejor estimación de la incertidumbre de medida.

Conclusión

Es conveniente hacer uso adecuado la ecuación (6) y no desestimar las interpolaciones entre las variables de influencia a fin de realizar las aportaciones adecuadas de la incertidumbre de medición. Particularmente, el sobre estimar la incertidumbre podría llevar a tener un resultado erróneo en comparaciones interlaboratorios (Ekici y Avci, 2023). De la Tabla 2, se observó que la variabilidad por repetibilidad para los instrumentos involucrados en este estudio no era significativa, lo que conlleva a atribuir los cambios al deterioro instrumental y modificación de la función de densidad rectangular. Se concluye que la aportación rectangular de la función de densidad de termómetro puede generar contribuciones a la incertidumbre a medida que el termopar de acoplamiento genera variaciones en las mediciones, como se observó en las diferencias entre las Tablas 3 y 4.

Agradecimientos

Agradecemos el apoyo de la Coordinación de Investigación Científica de la Universidad Michoacana de San Nicolás de Hidalgo.

Referencias

• Bianchi, D., Secco, N. (2021). Misconceptions about the Central Limit Theorem in Uncertainty-based Design Optimization. In AIAA Scitech 2021 Forum, 1594.
• Carbone, P., Macii, D., Petri, D. (2001). Measurement uncertainty and metrological confirmation in documented quality systems. In Proc. IMEKO TC4 Symposium, 2: 437-441.
• Cox, M., O’Hagan, A. (2022). Meaningful expression of uncertainty in measurement. Accreditation and Quality Assurance, 27(1): 19-37.
• Damasceno, J.C., Couto, P.R. (2018). Methods for evaluation of measurement uncertainty. (Vol. 2). London, UK: IntechOpen.
• Demeyer, S., Fischer, N., Elster, C. (2022). Guidance on Bayesian uncertainty evaluation for a class of GUM measurement models. Metrologia, 58(1): 014001.
• Ekici, C., Avci, Ö. (2023). An International Bilateral Inter-Laboratory Temperature Comparison Measurement. MAPAN, 38(3): 569-572.
• Internationale, O., Metrology, O. L. (2007). Guidance ILAC-G24 International. OIML, D(10).
• Kirkup, L., Frenkel, R.B. (2006). An introduction to uncertainty in measurement: using theGUM (guide to the expression of uncertainty in measurement). Cambridge University Press.
• Le Maître, O.P., Knio, O.M. (2010). Introduction: Uncertainty quantification and propagation. In Spectral methods for uncertainty quantification, 1-13.
• Masharipov, S.M., Mavlyanov, M.A., Abdumajidov, I.B. (2024). Metrological requirements of international standard ISO/IEC 17025: 2017 and experimental study questions on metrological traceability of measurement results. En A. Publishing (Ed.), Conference Proceedings, 2969, No. 1.
• Montgomery, D.C. (2019). Introduction to statistical quality control. John wiley & sons.
• Velychko, O., Gordiyenko, T. (2019). Metrological traceability at different measurement levels. In Standards, Methods and Solutions of Metrology. IntechOpen. IntechOpen.

Séptimo Congreso Nacional de Tecnología 16, 17 y 18 de octubre de 2024,
celebrado en formato virtual

---

Excepto donde se indique lo contrario esta obra está bajo una licencia Creative Commons Atribución No comercial, No derivada, 4.0 Internacional (CC BY NC ND 4.0 INTERNACIONAL).
https://creativecommons.org/licenses/by-nc-nd/4.0/deed.es

FORMA SUGERIDA DE CITAR:

Estevez-Delgado, G., Estevez-Delgado, J., y Cuevas-Cuevas, J. E. (2024). PERTURBACIÓN EN LA DISTRIBUCIÓN RECTANGULAR EN LA ESTIMACIÓN DE LA INCERTIDUMBRE DE MEDIDA. MEMORIAS DEL CONGRESO NACIONAL DE TECNOLOGÍA (CONATEC), Año 7, No. 7, septiembre 2024 - agosto 2025. Facultad de Estudios Superiores Cuautitlán. UNAM https://tecnicosacademicos.cuautitlan.unam.mx/CongresoTA/memorias2024/Mem2024_Paper10.html